在空间直角坐标系中.已知点A.若点M在y轴上.且|MA|=|MB|.则M的坐标是．题目和参考答案——青夏教育精英家教网—

题目内容

18．在空间直角坐标系中，已知点A（1，0，2），B（1，-3，1），若点M在y轴上，且|MA|=|MB|，则M的坐标是（0，-1，0）．

分析设出点M（0，y，0），由|MA|=|MB|，建立关于参数y的方程，求y值即可．

解答解：设设M（0，y，0），由|MA|=|MB|，
可得$\sqrt{{1}^{2}{+y}^{2}{+2}^{2}}$=$\sqrt{{1}^{2}{+（y+3）}^{2}{+1}^{2}}$，
即y²+5=（y+3）²+2，解得：y=-1．
M的坐标是（0，-1，0）．
故答案为：（0，-1，0）．

点评本题考点是点、线、面间的距离计算，空间两点距离公式的应用，考查计算能力．

练习册系列答案

相关题目

8．

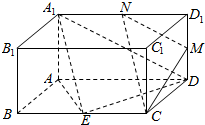如图，长方体ABCD-A₁B₁C₁D₁中，AA₁=AB=1，AD=2，E为BC的中点，点M，N分别为棱DD₁，A₁D₁的中点．
（Ⅰ）求证：平面CMN∥平面A₁DE；
（Ⅱ）求证：平面A₁DE⊥平面A₁AE．

9．下列函数中，是奇函数且在（0，1]上单调递减的函数是（　　）

6．已知集合A={x|x²+x+p=0}．
（Ⅰ）若A=∅，求实数p的取值范围；
（Ⅱ）若A中的元素均为负数，求实数p的取值范围．

13．若变量x，y满足约束条件$\left\{\begin{array}{l}{y≤2x}\\{x+y≤2}\\{y≥-2}\end{array}\right.$，则z=x-2y的最小值为-2．

3．已知函数f（x）=2$\sqrt{3}$sinxcosx+2cos²x-1，在△ABC中，内角A，B，C的对边分别为a，b，c，且f（B）=1．
（Ⅰ）求B；
（Ⅱ）若$\overrightarrow{BA}$•$\overrightarrow{BC}$=3，求b的取值范围．

10．

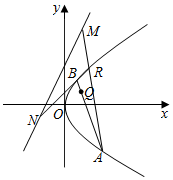已知抛物线C的方程为y²=2px（p＞0），抛物线的焦点到直线l：y=2x+2的距离为$\frac{4\sqrt{5}}{5}$．
（Ⅰ）求抛物线C的方程；
（Ⅱ）设点R（x₀，2）在抛物线C上，过点Q（1，1）作直线交抛物线C于不同于R的两点A，B，若直线AR，BR分别交直线l于M，N两点，求|MN|最小时直线AB的方程．

7．已知向量$\overrightarrow a$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$，$\overrightarrow{a}$=（2，0），|$\overrightarrow{b}$|=1，则|$\overrightarrow{a}$-2$\overrightarrow{b}$|=（　　）

8．讨论函数y=$\frac{1}{3}$x³+x²+ax+c的单调区间．

试题分类