题目内容
已知函数 ,
, .
.
(1)设 是函数
是函数 图象的一条对称轴,求
图象的一条对称轴,求 的值.
的值.
(2)求函数 的单调递增区间.
的单调递增区间.
(1) 或
或 ,(2)
,(2) (
( ).
).
解析试题分析:(1)先将三角函数化为基本三角函数,即利用降幂公式得 ,再利用基本三角函数性质得:
,再利用基本三角函数性质得:
 ,即
,即 ,所以
,所以 .因此分
.因此分 为奇偶讨论得,
为奇偶讨论得, 的值为
的值为 或
或 ,(2)同样先将三角函数化为基本三角函数,此时要用到两角和余弦公式及配角公式,即
,(2)同样先将三角函数化为基本三角函数,此时要用到两角和余弦公式及配角公式,即

 ,再利用基本三角函数性质得:
,再利用基本三角函数性质得: ,即
,即 (
( ),故函数
),故函数 的单调递增区间是
的单调递增区间是 (
( ).
).
试题解析:(1)由题设知 .
.
因为 是函数
是函数 图象的一条对称轴,所以
图象的一条对称轴,所以
 ,
,
即 (
( ).所以
).所以 .
.
当 为偶数时,
为偶数时, ,
,
当 为奇数时,
为奇数时, .
.
(2)

 .
.
当 ,即
,即 (
( )时,
)时,
函数 是增函数,
是增函数,
故函数 的单调递增区间是
的单调递增区间是 (
( ).
).
考点:三角函数性质

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知函数 (A>0,ω>0)的一系列对应值如下表:
(A>0,ω>0)的一系列对应值如下表:
| x | 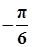 |  | 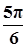 | 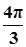 |  |  | 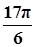 |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
(1)根据表格提供的数据求函数f(x)的一个解析式;
(2)根据(1)的结果,若函数
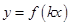 (k>0)周期为
(k>0)周期为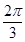 ,当x∈[0,
,当x∈[0, ]时,方程
]时,方程 恰有两个不同的解,求实数m的取值范围;
恰有两个不同的解,求实数m的取值范围; 
 的最小正周期;
的最小正周期; 时,求函数f(x)的单调区间。
时,求函数f(x)的单调区间。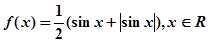
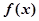 的周期T,与单调增区间.
的周期T,与单调增区间.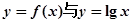 的图象有几个公共交点.
的图象有几个公共交点.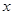 的函数
的函数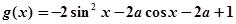 的最小值为
的最小值为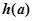 ,试确定满足
,试确定满足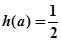 的
的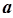 的值,并对此时的
的值,并对此时的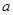 值求
值求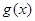 的最小值.
的最小值.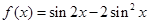
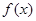 的最小正周期。
的最小正周期。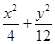 =1上在第一象限的点,A(2,0),B(0,2
=1上在第一象限的点,A(2,0),B(0,2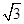 )
) 的终边经过点
的终边经过点 ,且
,且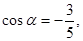
 的值.(2)求
的值.(2)求 与
与 的值.
的值.
 的最大值,并写出
的最大值,并写出 时的取值集合;
时的取值集合; 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 求
求 的最小值.
的最小值. )的部分图象如图所示.
)的部分图象如图所示.
 的单调递增区间.
的单调递增区间.