题目内容
9.a1=1,an+1-an=4n+5,则an=2n2+3n-4.分析 根据题中已知条件先求出an-an-1的值,进而可以求出数列{an}的通项公式.
解答 解:∵an+1-an=4n+5,a1=1
∴a2-a1=4×1+5,
a3-a2=4×2+5,
…
an-an-1=4(n-1)+5,
将上面各等式相加,得an-a1=4+8+…+4(n-1)+5(n-1)=$\frac{(n-1)(4+4n-4)}{2}$+5(n-1),
∴an=2n2+3n-4,
当n=1时,也符合上式,
∴an=2n2+3n-4,
故答案为:2n2+3n-4.
点评 本题考查了等差数列的基本知识,累和法求通项公式,考查了学生的计算能力,解题时要认真审题,仔细解答,避免错误,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
17.阅读如图的程序框图,运行相应的程序,若输入x的值为1,则输出S的值为( )


| A. | 21 | B. | 57 | C. | 64 | D. | 73 |
4.执行如图所示的程序框图,输出c的结果为( )
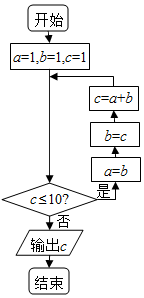

| A. | 13 | B. | 21 | C. | 17 | D. | 15 |
1.若an>0,a1=2,且当n≥2时,有an+an-1=$\frac{n}{{a}_{n}-{a}_{n-1}}$+2,求数列{$\frac{1}{({a}_{n}-1)^{2}}$}的所有项之和.
19.与25°角终边相同的角是( )
| A. | 385° | B. | -325° | C. | 335° | D. | -685° |