题目内容
如图,矩形 所在的半平面和直角梯形
所在的半平面和直角梯形 所在的半平面成
所在的半平面成 的二面角,
的二面角, ∥
∥ ,
, ,
, ,
, ,
, ,
, .
.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)在线段 上求一点
上求一点 ,使锐二面角
,使锐二面角 的余弦值为
的余弦值为 .
.

(Ⅰ)因为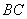 ∥
∥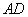 ,
,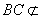 平面
平面 ,所以
,所以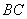 ∥平面
∥平面 ,
,
同理 ∥平面
∥平面 ,又因为
,又因为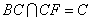 ,所以平面
,所以平面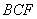 ∥平面
∥平面 ,
,
而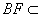 平面
平面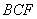 ,所以
,所以 ∥平面
∥平面 . ………………………………………5分
. ………………………………………5分
(Ⅱ)因为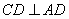 ,
, 所以
所以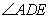 就是二面角
就是二面角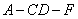 的平面角,为
的平面角,为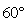 , ……………………………………………………………………………………6分
, ……………………………………………………………………………………6分
又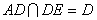 ,所以
,所以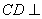 平面
平面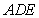 ,平面
,平面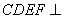 平面
平面 ,
,
 作
作 于
于 ,则
,则 ,…………7分
,…………7分
连结 ,在
,在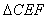 中由余弦定理求得
中由余弦定理求得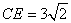 ,
,
易求得, ,
,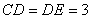 ,
, ,
,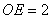 . ……………………………………………8分
. ……………………………………………8分
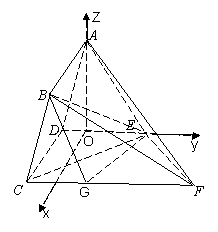
以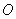 为原点,以平行于
为原点,以平行于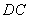 的直线为
的直线为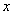 轴,以直线
轴,以直线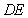 为
为
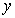 轴,建立如图空间直角坐标系
轴,建立如图空间直角坐标系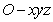 ,
,
则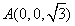
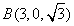 ,
,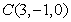 ,
,
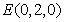 ,
,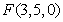 ,
,
设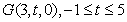 ,
,
则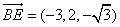 ,
,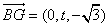 ,
,
设平面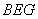 的一个法向量为,
的一个法向量为,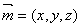 ,
,
则由 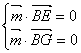 得,
得,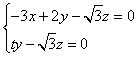 ,
,
取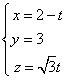 得,
得, 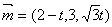 , …………………………………………10分
, …………………………………………10分
平面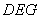 的一个法向量
的一个法向量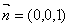 , …………………………………………11分
, …………………………………………11分
所以,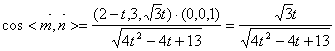 , ………12分
, ………12分
为使锐二面角 的余弦值为
的余弦值为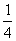 ,只需
,只需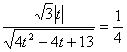 ,
,
解得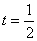 ,此时
,此时 , …………………………………………………13分
, …………………………………………………13分
即所求的点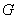 为线段
为线段 的靠近
的靠近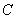 端的四分之一分点. …………………………14分
端的四分之一分点. …………………………14分

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 的图象与直线
的图象与直线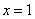 的交点个数为0或1;
的交点个数为0或1;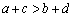 ”是“
”是“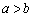 且
且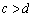 ”的充分而不必要条件;
”的充分而不必要条件;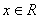 ,使得
,使得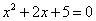 ”的否定是“对任意
”的否定是“对任意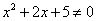 ”.
”. ,且
,且 ,则角
,则角 的取值范围是 .
的取值范围是 . 和
和 ,其中,
,其中,  ,它们所表示的曲线可能是下列图象中的
,它们所表示的曲线可能是下列图象中的 A. B. C. D.
A. B. C. D. 轴上,左、右焦点分别为
轴上,左、右焦点分别为 ,且它们在第一象限的交点为
,且它们在第一象限的交点为 ,
, 是以
是以 为底边的等腰三角形,若双曲线的离心率的取值范围为
为底边的等腰三角形,若双曲线的离心率的取值范围为 .则该椭圆的离心率的取值范围是 .
.则该椭圆的离心率的取值范围是 . ,则
,则 的值是( )
的值是( ) B.1 C.
B.1 C. D.2
D.2 ,
, ,
, 不共线,且两两之间的夹角都为
不共线,且两两之间的夹角都为 ,若|
,若|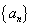 中,
中, ,则
,则
 的图象向左平移
的图象向左平移 个单位,若所得图象与原图象重合,则
个单位,若所得图象与原图象重合,则 的值不可能等于( )
的值不可能等于( )