题目内容
【题目】函数
的定义域为
，若存在一次函数
，使得对于任意的
，都有
恒成立，则称函数
在上的弱渐进函数.下列结论正确的是______．（写出所有正确命题的序号）
①
是
在
上的弱渐进函数；
②
是
在上的弱渐进函数；
③
是
在上的弱渐进函数；
④
是
在上的弱渐进函数.
【答案】①④
【解析】
根据弱渐进函数的新定义，对4个命题分别构建
①构建关系，并分子有理化，由不等式性质可知符合题意，正确；
②构建关系，由双勾函数值域可知不符合题意，错误；
③构建关系，取特值
，其绝对值大于1，不符合题意，错误；
④构建关系，求导分析单调性，求得值域，符合题意，正确.
①由于
，所以
，所以
，所以①正确；
②设
，当
时，
，不符合
，所以②错误；
③设
，
，
，不符合
，所以③错误；
④设
，
，当时，
，在
上单调递减，所以
；又时，
，
，即
，所以
，④正确，综上，①④正确.
故答案为：①④
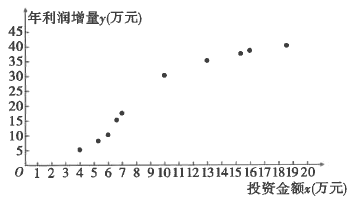
【题目】某果园种植“糖心苹果”已有十余年,为了提高利润,该果园每年投入一定的资金,对种植采摘包装宣传等环节进行改进.如图是2009年至2018年,该果园每年的投资金额
(单位:万元)与年利润增量
(单位:万元)的散点图:
该果园为了预测2019年投资金额为20万元时的年利润增量,建立了关于的两个回归模型;
模型①:由最小二乘公式可求得与的线性回归方程:
;
模型②:由图中样本点的分布,可以认为样本点集中在曲线:
的附近,对投资金额做交换,令
,则
,且有
,
,
,
.
(1)根据所给的统计量,求模型②中关于的回归方程;
(2)分别利用这两个回归模型,预测投资金额为20万元时的年利润增量(结果保留两位小数);
(3)根据下列表格中的数据,比较两种模型的相关指数
,并说明谁的预测值精度更高更可靠.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 102.28 | 36.19 |
附:样本
的最小乘估计公式为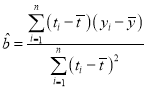
,
;
相关指数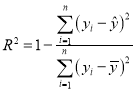
.
参考数据:
,
.
