题目内容
(1)已知α为锐角,且tanα=| 1 |
| 2 |
| sin2αcosα-sinα |
| sin2αcos2α |
(2)化简:
| 1+sin2α-cos2α |
| 1+sin2α+cos2α |
分析:(1)由α锐角,及tanα的值,利用同角三角函数间的基本关系求出cosα的值,然后把所求的式子中的sin2α利用二倍角的正弦函数公式化简,分子提取sinα后,利用二倍角的余弦函数公式变形,与分母约分可得关于cosα的式子,把cosα的值代入即可得到原式的值;
(2)把原式的分子与分母中的第一与第三项结合,利用二倍角的余弦函数公式化简,分子分母的第二项利用二倍角的正弦函数公式变形,然后分子提取2sinα,分母提取2cosα,约分后利用同角三角函数间的基本关系即可得到化简结果.
(2)把原式的分子与分母中的第一与第三项结合,利用二倍角的余弦函数公式化简,分子分母的第二项利用二倍角的正弦函数公式变形,然后分子提取2sinα,分母提取2cosα,约分后利用同角三角函数间的基本关系即可得到化简结果.
解答:解:(1)由α为锐角,且tanα=
,
得到cosα=
=
=
则
=
=
=
=
=
;
(2)
=
=
=
=tanα.
| 1 |
| 2 |
得到cosα=
| 1 |
| secα |
| 1 | ||
|
2
| ||
| 5 |
则
| sin2αcosα-sinα |
| sin2αcos2α |
=
| 2sinαcos2α-sinα |
| 2sinαcosαcos2α |
=
| sinα(2cos2α-1) |
| 2sinαcosαcos2α |
=
| sinαcos2α |
| 2sinαcosαcos2α |
=
| 1 |
| 2cosα |
=
| ||
| 4 |
(2)
| 1+sin2α-cos2α |
| 1+sin2α+cos2α |
=
| sin2α+(1-cos2α) |
| sin2α+(1+cos2α) |
=
| 2sinαcosα+2sin2α |
| 2sinαcosα+2cos2α |
=
| 2sinα(sinα+cosα) |
| 2cosα(sinα+cosα) |
=tanα.
点评:此题考查了二倍角的正弦、余弦函数公式,以及同角三角函数间的基本关系,熟练掌握二倍角的正弦、余弦函数公式是解本题的关键.

练习册系列答案
相关题目

 ,cos(α+β)=-
,cos(α+β)=- ,求β;
,求β; +α)=
+α)= ,求
,求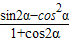 的值.
的值. ,cos(α+β)=-
,cos(α+β)=- ,求β;
,求β; +α)=
+α)= ,求
,求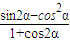 的值.
的值.