题目内容
如图2-1-21,已知AD为锐角△ABC的外接圆O的直径,AE⊥BC于E,交外接圆于F,
图2-1-21
(1)求证:∠1=∠2;
(2)求证:AB·AC=AE·AD;
(3)作OH⊥AB,垂足为H.求证:![]() .
.
思路分析:(1)∠1与∠2均为圆周角,要证它们相等,只需证所对的弧相等,弧BD与弧FC夹在BC与DF之间,只需证DF∥BC即可.?
(2)要证等积式,可先证比例式![]() =
=![]() ,而这可由△ABD∽△AEC证得.?
,而这可由△ABD∽△AEC证得.?
(3)要证![]() ,联想到中位线定理,可先证
,联想到中位线定理,可先证![]() .
.
证明:(1)连结DF,∵AD为直径,∴∠AFD =90°.?
又BC⊥AF,∴DF∥BC.?
∴![]() =
=![]() .∴∠1=∠2.?
.∴∠1=∠2.?
(2)连结BD,∵AD为直径,∴∠ABD =90°.?
又AE⊥BC,∴∠AEC=90°.?
∴∠ABD =∠AEC.?
又∠1=∠2,?
∴△ABD∽△AEC(或由∠1=∠2,∠ACB =∠ADB可知△ABD∽△AEC).?
∴![]() =
=![]() ,?
,?
即AB·AC =AE·AD.?
(3)连结CF,∵AD为直径,∴∠ABD =90°.?
又OH⊥AB,∴OH∥BD.?
∴H为AB中点,即OH为△ABD的中位线.?
∴![]() .?
.?
又![]() =
=![]() ,∴BD =CF.?
,∴BD =CF.?
∴![]() .
.

己知在锐角ΔABC中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]()
(I )求角![]() 大小;
大小;
(II)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.

20.如图1,在平面内,![]() 是
是![]() 的矩形,
的矩形,![]() 是正三角形,将
是正三角形,将![]() 沿
沿![]() 折起,使
折起,使![]() 如图2,
如图2,![]() 为
为![]() 的中点,设直线
的中点,设直线![]() 过点
过点![]() 且垂直于矩形
且垂直于矩形![]() 所在平面,点
所在平面,点![]() 是直线
是直线![]() 上的一个动点,且与点
上的一个动点,且与点![]() 位于平面
位于平面![]() 的同侧。
的同侧。
(1)求证:![]() 平面
平面![]() ;
;
(2)设二面角![]() 的平面角为
的平面角为![]() ,若
,若![]() ,求线段
,求线段![]() 长的取值范围。
长的取值范围。


21.已知A,B是椭圆![]() 的左,右顶点,
的左,右顶点,![]() ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线![]() 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
(1)求椭圆C的方程;
 (2)求三角形MNT的面积的最大值
(2)求三角形MNT的面积的最大值
22. 已知函数![]()
![]() ,
,
(Ⅰ)若![]() 在
在![]() 上存在最大值与最小值,且其最大值与最小值的和为
上存在最大值与最小值,且其最大值与最小值的和为![]() ,试求
,试求![]() 和
和![]() 的值。
的值。
(Ⅱ)若![]() 为奇函数:
为奇函数:
(1)是否存在实数![]() ,使得
,使得![]() 在
在![]() 为增函数,
为增函数,![]() 为减函数,若存在,求出
为减函数,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)如果当![]() 时,都有
时,都有![]() 恒成立,试求
恒成立,试求![]() 的取值范围.
的取值范围.
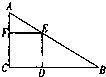 如图所示,已知在△ABC中,∠C=90°,正方形DEFC内接于△ABC,DE∥AC,EF∥BC,AC=1,BC=2,则AF:FC=
如图所示,已知在△ABC中,∠C=90°,正方形DEFC内接于△ABC,DE∥AC,EF∥BC,AC=1,BC=2,则AF:FC=