题目内容
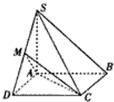 (2012•西区模拟)如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB,M是SD的中点.
(2012•西区模拟)如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB,M是SD的中点.(1)求证:SB∥平面ACM;
(2)求二面角D-AC-M的大小.
分析:(1)连接BD交AC于E,连接ME,由ABCD是正方形,知E是BD的中点,由M是SD的中点,知ME是△DSB的中位线,故ME∥SB,由此能够证明SB∥平面ACM.
(2)取AD的中点F,则MF∥SA,作FQ⊥AC于Q,连接MQ,由SA⊥底面ABCD,知MF⊥底面ABCD,故FQ为MQ在平面ABCD内的射影,由FQ⊥AC,知∠FQM为二面角D-AC-M的平面角,由此能求出二面角D-AC-M的大小.
(2)取AD的中点F,则MF∥SA,作FQ⊥AC于Q,连接MQ,由SA⊥底面ABCD,知MF⊥底面ABCD,故FQ为MQ在平面ABCD内的射影,由FQ⊥AC,知∠FQM为二面角D-AC-M的平面角,由此能求出二面角D-AC-M的大小.
解答: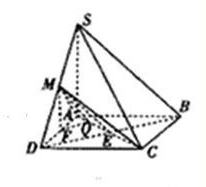 (1)证明:连接BD交AC于E,连接ME,
(1)证明:连接BD交AC于E,连接ME,
∵ABCD是正方形,∴E是BD的中点,
∵M是SD的中点,∴ME是△DSB的中位线,∴ME∥SB,
∵ME?平面ACM,SB?平面ACM,
∴SB∥平面ACM.
(2)解:取AD的中点F,则MF∥SA,作FQ⊥AC于Q,连接MQ,
∵SA⊥底面ABCD,∴MF⊥底面ABCD,
∴FQ为MQ在平面ABCD内的射影,
∵FQ⊥AC,∴MQ⊥AC,∴∠FQM为二面角D-AC-M的平面角,
设SA=AB=a,在Rt△MFQ中,MF=
SA=
,FQ=
DE=
a,
∴tan∠FQM=
=
,
∴二面角D-AC-M的大小为arctan
.
 (1)证明:连接BD交AC于E,连接ME,
(1)证明:连接BD交AC于E,连接ME,∵ABCD是正方形,∴E是BD的中点,
∵M是SD的中点,∴ME是△DSB的中位线,∴ME∥SB,
∵ME?平面ACM,SB?平面ACM,
∴SB∥平面ACM.
(2)解:取AD的中点F,则MF∥SA,作FQ⊥AC于Q,连接MQ,
∵SA⊥底面ABCD,∴MF⊥底面ABCD,
∴FQ为MQ在平面ABCD内的射影,
∵FQ⊥AC,∴MQ⊥AC,∴∠FQM为二面角D-AC-M的平面角,
设SA=AB=a,在Rt△MFQ中,MF=
| 1 |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
∴tan∠FQM=
| ||||
|
| 2 |
∴二面角D-AC-M的大小为arctan
| 2 |
点评:本题考查直线与平面平等的证明,考查二面角大小的求法,解题时要认真审题,注意挖掘题设中的隐含条件,合理地化空间问题为平面问题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 (2012•西区模拟)如图,三棱锥P-ABC中,PA⊥平面ABC,PA=2,△ABC是边长为
(2012•西区模拟)如图,三棱锥P-ABC中,PA⊥平面ABC,PA=2,△ABC是边长为