题目内容
在△ABC中,A、B、C所对的边分别是a、b、c,bcos B是acos C,ccos A的等差中项.
(1)求B的大小;
(2)若 ,求△ABC的面积.
,求△ABC的面积.
(1) (2)
(2)
解析试题分析:(1)由已知条件acos C+ccos A=2bcos B,利用正弦定理化边为角的正弦,得:sin Acos C+cos Asin C=2sin Bcos B.逆用两角和的正弦公式得sin(A+C)=2sin Bcos B.
根据三角形内角和为π,及角B的范围求得 .
.
(2)由 ,再根据余弦定理得
,再根据余弦定理得 可得
可得 .
.
利用面积公式得 .
.
试题解析:(1)由题意,得acos C+ccos A=2bcos B.
由正弦定理化边为角,得sin Acos C+cos Asin C=2sin Bcos B,
即sin(A+C)=2sin Bcos B.
∵A+C=π-B,0<B<π,∴sin(A+C)=sin B≠0.
∴ ,∴
,∴
(2)由 ,得
,得
即 ,把
,把 带入得
带入得 .∴
.∴ .
.
考点:解三角形

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 .已知
.已知
 ,求△ABC外接圆半径.
,求△ABC外接圆半径. 中,内角
中,内角 的对边分别为
的对边分别为 ,已知
,已知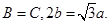
 的值;(2)
的值;(2) 的值.
的值. 的三个内角
的三个内角 成等差数列,它们的对边分别为
成等差数列,它们的对边分别为 ,且满足
,且满足 ,
, .
. ;
; .
. 分别为
分别为 的三个内角
的三个内角 的对边,且
的对边,且 .
. 的大小; (2)若
的大小; (2)若 ,
,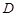 为
为 的中点,求
的中点,求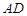 的长.
的长. 中,
中, ,
, ,
, .
. 长;
长; 的值.
的值.
 的内角
的内角 所对边的长分别是
所对边的长分别是 ,且
,且
 的值;
的值; 的值.
的值. ,则
,则 .
.