Question

【题目】在中，，点在边上，且.

（1）若，求；

（2）若，求的周长.

Answer 1

【答案】(1) .

(2) .

【解析】分析：首先应用题中条件，结合余弦定理求得，第一问利用余弦定理和正弦定理，以及结合边的关系，求得以及，结合同角三角函数关系式，求得的值，第二问结合边的关系，结合余弦定理求得其周长的值.

详解：解法一：如图，已知，，

所以，则.

在△中，根据余弦定理，，

所以.

（1）在△中，，，，

由余弦定理，

所以，解得，所以，

在△中，由正弦定理，

所以，，

由，，，在△中，由，得

，故，

所以 ，

所以

（2）设，则，从而，

故．

在△中，由余弦定理得，

因为 ，所以，解得．

所以．故△周长为．

解法二：如图，已知，，所以，则.

在△中，根据余弦定理，，

所以.

（1）在△中，，，，

由余弦定理，

所以，解得，

由余弦定理，

又因为，所以．

所以，

所以．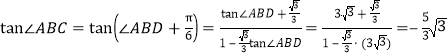

（2）同解法一．