题目内容
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)已知A、B是椭圆C的左、右顶点,动点M满足MB⊥AB,连接AM交椭圆于点P,在x轴上是否存在异于点A、B的定点Q,使得以MP为直径的圆经过直线BP和直线MQ的交点,若存在,求出Q点,若不存在,说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出
,由此能求出椭圆方程.
(2)设P(x0,y0),则直线AP的方程y=
(x+2),由已知条件推导出M(2,
),设定点Q(m,0),由MQ⊥PB,得到
•
=-1,由此能求出定点Q(1,0).
|
(2)设P(x0,y0),则直线AP的方程y=
| y0 |
| x0+2 |
| 4y0 |
| x0+2 |
| y02 |
| x02-4 |
| 4 |
| 2-m |
解答:
解:(1)∵椭圆C:
+
=1(a>b>0)过点(
,
)且离心率为
,
∴
,解得a=2,b=1,
∴椭圆方程为
+y2=1.
(2)设P(x0,y0),则直线AP的方程y=
(x+2),
∵A、B是椭圆C:
+y2=1的左、右顶点,动点M满足MB⊥AB,
∴M(2,
),
设定点Q(m,0),∵MQ⊥PB,
∴kMQ•kPB=-1,即
•
=-1,
∴
•
=-1,
又∵
+y02=1,∴
=
=-
,
∴-
•
=-1,解得m=1,
∴定点Q(1,0).
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
|
∴椭圆方程为
| x2 |
| 4 |
(2)设P(x0,y0),则直线AP的方程y=
| y0 |
| x0+2 |

∵A、B是椭圆C:
| x2 |
| 4 |
∴M(2,
| 4y0 |
| x0+2 |
设定点Q(m,0),∵MQ⊥PB,
∴kMQ•kPB=-1,即
| ||
| 2-m |
| y0 |
| x0-2 |
∴
| y02 |
| x02-4 |
| 4 |
| 2-m |
又∵
| x02 |
| 4 |
| y02 |
| x02-4 |
1-
| ||
| x02-4 |
| 1 |
| 4 |
∴-
| 1 |
| 4 |
| 4 |
| 2-m |
∴定点Q(1,0).
点评:本题考查椭圆方程的求法,考查满足条件的定点坐标是否存在的判断与求法,解题时要认真审题,注意直线与椭圆的位置关系的灵活运用.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
在区间[0,π]内随机取两个数分别记为a、b,则使得函数f(x)=x2+2ax-b2+π有零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
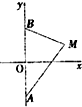 已知点A、B的坐标分别是(0,-1),(0,1),直线AM、BM相交于点M,且它们的斜率之积为-
已知点A、B的坐标分别是(0,-1),(0,1),直线AM、BM相交于点M,且它们的斜率之积为-