题目内容
5.将函数y=cos4x+sin2x-$\frac{7}{8}$(x∈R)图象向右平移m(m>0)个单位长度后,所得到的图象关于原点对称,则m的最小值为( )| A. | $\frac{π}{8}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性,求得m的最小值.
解答 解:将函数y=cos4x+sin2x-$\frac{7}{8}$=${(\frac{1+cos2x}{2})}^{2}$+$\frac{1-cos2x}{2}$-$\frac{7}{8}$=$\frac{{cos}^{2}2x}{4}$-$\frac{1}{8}$=$\frac{1+cos4x}{8}$-$\frac{1}{8}$=$\frac{1}{8}$cos4x
的图象向右平移m(m>0)个单位长度后,可得函数y=$\frac{1}{8}$cos4(x-m)=$\frac{1}{8}$cos(4x-4m)的图象,
根据所得到的图象关于原点对称,可得4m=kπ+$\frac{π}{2}$,即 m=$\frac{kπ}{4}$+$\frac{π}{8}$,k∈Z,
则m的最小值为$\frac{π}{8}$,
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
15.随机变量X~N(μ,σ2),F(x)为分布函数,Y=F(x),则概率P(Y$≤\frac{1}{2}$)( )
| A. | 与μ,σ有关; | B. | 与μ有关,与σ无关; | ||
| C. | 与σ有关,与μ无关; | D. | 与μ,σ无关. |
16.已知直线ax+3y-1=0与直线3x-y+2=0互相垂直,则a=( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
20.为了增强消防安全意识,某中学对全体学生做了一次消防知识讲座,从男生中随机抽取50人,从女生中随机抽取70人参加消防知识测试,统计数据得到如下列联表:
(Ⅰ)试判断是否有90%的把握认为消防知识的测试成绩优秀与否与性别有关;
附:
K2=$\frac{a(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
(Ⅱ)为了宣传消防安全知识,从该校测试成绩获得优秀的同学中采用分层抽样的方法,随机选出6名组成宣传小组.现从这6人中随机抽取2名到校外宣传,求到校外宣传的同学中至少有1名是男生的概率.
| 优秀 | 非优秀 | 总计 | |
| 男生 | 15 | 35 | 50 |
| 女生 | 30 | 40 | 70 |
| 总计 | 45 | 75 | 120 |
附:
K2=$\frac{a(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
15.曲线(x+2y+a)(x2-y2)=0为平面上交于一点的三条直线的充要条件是( )
| A. | a=0 | B. | a=1 | C. | a=-1 | D. | a∈R |
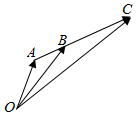 已知A(2,3),B(5,4),连接AB并延长至C,使得AC=3AB,求C点的坐标.(提示:如图所示,$\overrightarrow{OC}$=$\overrightarrow{OA}$+3$\overrightarrow{AB}$)
已知A(2,3),B(5,4),连接AB并延长至C,使得AC=3AB,求C点的坐标.(提示:如图所示,$\overrightarrow{OC}$=$\overrightarrow{OA}$+3$\overrightarrow{AB}$)