题目内容
在数列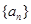 中,
中,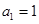 ,
,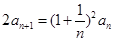 .
.
(1)求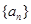 的通项公式;
的通项公式;
(2)令 ,求数列
,求数列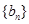 的前
的前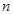 项和
项和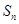 .
.
(1) .(2)
.(2) .
.
解析试题分析:(1)由条件得 ,又
,又 时,
时, ,
,
故数列 构成首项为1,公式为
构成首项为1,公式为 的等比数列.从而
的等比数列.从而 ,即
,即 . 6分
. 6分
(2)由 得
得 ,
, ,
,
两式相减得 :  , 所以
, 所以  . 12分
. 12分
考点:本题主要考查等差数列、等比数列的的基础知识,“错位相减法”求和。
点评:中档题,本题具有较强的综合性,本解答从确定通项公式入手,认识到数列的特征,利用“错位相消法”达到求和目的。“分组求和法”“裂项相消法”“错位相减法”是高考常常考到数列求和方法。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
数列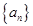 中,
中,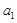 =2,
=2, ,则
,则 =( ).
=( ).
| A.2+ln n | B.2+ (n-1) ln n | C.2+ n ln n | D.1+n+ln n |
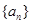 的前
的前 项和
项和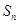 ,满足:
,满足: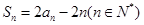 .
.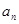 ;
;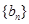 的满足
的满足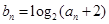 ,
,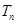 为数列
为数列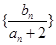 的前
的前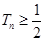 .
.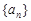 满足:
满足: ,数列
,数列 满足
满足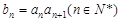 .
.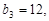 求
求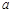 的值及
的值及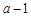 的等比数列,问是否存在正实数
的等比数列,问是否存在正实数 ,使得数列
,使得数列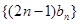 的前
的前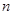 项和
项和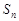 (用n,
(用n,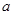 表示).
表示). 的前
的前 项和为
项和为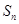 ,且
,且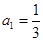 ,
,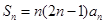
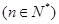 .
. 的值;
的值;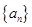 的前n项和记为
的前n项和记为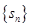 ,已知
,已知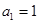 ,
,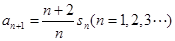 .
.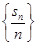 是等比数列;
是等比数列;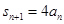 .
.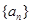 的前
的前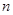 项和为
项和为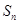 ,且有
,且有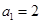 ,
,
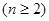 .
.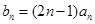 ,求数列
,求数列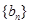 的前
的前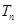 ;
;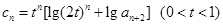 ,且数列
,且数列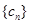 中的 每一项总小于它后面的项,求实数
中的 每一项总小于它后面的项,求实数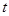 的取值范围.
的取值范围. 满足:
满足: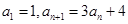 ;
;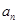 ;
;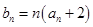 ,求数列
,求数列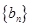 的前
的前 项和为
项和为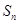 。
。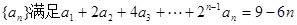 .
.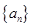 的通项公式;
的通项公式;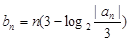 ,探求使
,探求使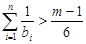 恒成立的
恒成立的 的最大整数值.
的最大整数值.