题目内容
已知数列 的前
的前 项和为
项和为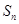 ,且
,且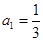 ,
,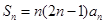
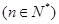 .
.
(1)求 的值;
的值;
(2)猜想 的通项公式,并用数学归纳法证明.
的通项公式,并用数学归纳法证明.
(1)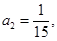
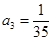 (2)通项为
(2)通项为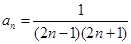 证明:①当
证明:①当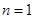 时,由条件知等式成立,②假设当
时,由条件知等式成立,②假设当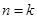 (
(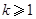 且
且 )等式成立,即:
)等式成立,即: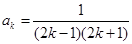
那么当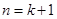 时,
时,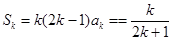 ,
,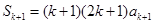 ,由
,由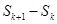 得
得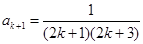 由①②可知,命题对一切
由①②可知,命题对一切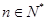 都成立
都成立
解析试题分析:⑴
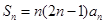 ,且
,且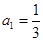
 当
当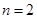 时,
时,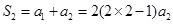 ,解得:
,解得: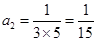 ;
;
当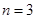 时,
时,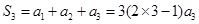 ,解得:
,解得: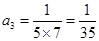
⑵由⑴可以猜想 的通项为
的通项为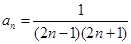
用数学归纳法证明如下:
①当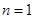 时,由条件知等式成立;
时,由条件知等式成立;
②假设当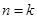 (
(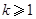 且
且 )等式成立,即:
)等式成立,即: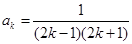
那么当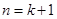 时,由条件
时,由条件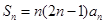 有:
有: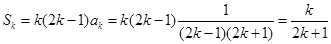 ;
; 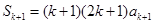

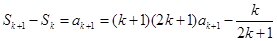 ,即
,即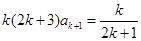 ,
, 
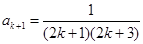 ,即:当
,即:当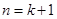 时等式也成立.
时等式也成立.
由①②可知,命题对一切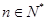 都成立.
都成立.
考点:数列求通项及数学归纳法证明
点评:已知条件是关于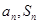 的关系式,此关系式经常用到
的关系式,此关系式经常用到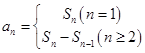
有关于正整数的命题常用数学归纳法证明,其主要步骤:第一步,n取最小的正整数时命题成立,第二步,假设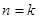 时命题成立,借此来证明
时命题成立,借此来证明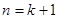 时命题成立
时命题成立

练习册系列答案
相关题目
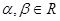 且
且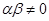 ,数列
,数列 满足
满足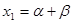 ,
,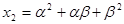 ,
,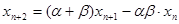 (
(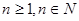 ),令
),令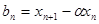 ,
,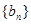 是等比数列;
是等比数列;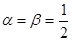 ,求
,求 项和
项和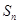 .
.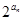 }的前n项和Sn.
}的前n项和Sn.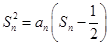 .
.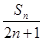 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.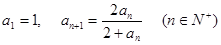 ,试猜想这个数列的通项公式。
,试猜想这个数列的通项公式。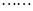
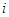 行里的最后一个数字是多少?
行里的最后一个数字是多少?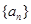 中,
中,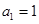 ,
,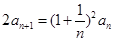 .
. ,求数列
,求数列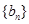 的前
的前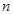 项和
项和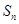 .
.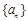 满足:
满足: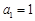 ,
,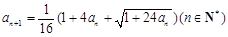 。
。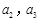 ;
; 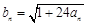 ,求数列
,求数列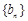 的通项公式;
的通项公式;