题目内容
先后2次抛掷一枚骰子,将得到的点数分别记为a,b.
(1)求直线ax+by+5=0与圆x2+y2=1相切的概率;
(2)将a,b,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
(1)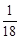 ;(2)
;(2)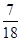
解析试题分析:(1)先后2次抛掷一枚骰子,将得到的点数分别记为a,b,事件总数为6×6=36.
∵直线ax+by+c=0与圆x2+y2=1相切的充要条件是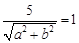 即:a2+b2=25,……2分
即:a2+b2=25,……2分
由于a,b∈{1,2,3,4,5,6}
∴满足条件的情况只有a=3,b=4,c=5;或a=4,b=3,c=5两种情况. ……4分
∴直线ax+by+c=0与圆x2+y2=1相切的概率是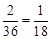 ……6分
……6分
(2)先后2次抛掷一枚骰子,将得到的点数分别记为a,b,事件总数为6×6=36.
∵三角形的一边长为5 ∴当a=1时,b=5,(1,5,5) 1种
当a=2时,b=5,(2,5,5) 1种
当a=3时,b=3,5,(3,3,5),(3,5,5) 2种
当a=4时,b=4,5,(4,4,5),(4,5,5) 2种
当a=5时,b=1,2,3,4,5,6, (5,1,5),(5,2,5),(5,3,5),
(5,4,5),(5,5,5),(5,6,5) 6种
当a=6时,b=5,6,(6,5,5),(6,6,5) 2种
故满足条件的不同情况共有14种 ……12分
答:三条线段能围成不同的等腰三角形的概率为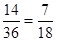 . ……14分
. ……14分
考点:本题考查了古典概型的应用,考查了学生分析问题解决问题的能力。
点评:对于古典概型的概率的计算,首先要分清基本事件总数及事件 包含的基本事件数,分清的方法常用列表法、画图法、列举法、列式计算等方法。
包含的基本事件数,分清的方法常用列表法、画图法、列举法、列式计算等方法。

 ABC考王全优卷系列答案
ABC考王全优卷系列答案(本小题满分12分)为了参加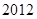 年贵州省高中篮球比赛,某中学决定从四个篮球较强的班级中选出
年贵州省高中篮球比赛,某中学决定从四个篮球较强的班级中选出 人组成男子篮球队代表所在地区参赛,队员来源人数如下表:
人组成男子篮球队代表所在地区参赛,队员来源人数如下表:
| 班级 | 高三(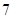 )班 )班 | 高三(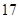 )班 )班 | 高二( )班 )班 | 高二( )班 )班 |
| 人数 |  | 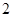 |  |  |
 名队员中随机选出两名,求两人来自同一班级的概率;(II)该中学篮球队经过奋力拼搏获得冠军.若要求选出两位队员代表冠军队发言,设其中来自高三(7)班的人数为
名队员中随机选出两名,求两人来自同一班级的概率;(II)该中学篮球队经过奋力拼搏获得冠军.若要求选出两位队员代表冠军队发言,设其中来自高三(7)班的人数为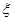 ,求随机变量
,求随机变量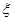 的分布列及数学期望
的分布列及数学期望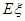 .
.  为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求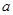 、
、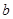 是常数,关于
是常数,关于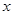 的一元二次方程
的一元二次方程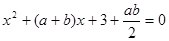 有实数解记为事件
有实数解记为事件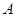 .
.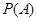 ;
;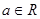 、
、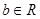 ,
,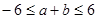 且
且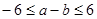 ,求
,求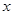 后放入乙盒,再从乙盒中任取一小球,记下号码
后放入乙盒,再从乙盒中任取一小球,记下号码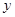 .
. 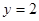 的概率;
的概率;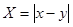 ,求随机变量
,求随机变量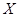 的分布列及数学期望.
的分布列及数学期望. 的一元二次方程
的一元二次方程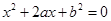 .
.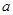 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数,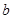 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;