题目内容
(本小题满分12分)盒中有大小相同的编号为1,2,3,4,5,6的六只小球,规定:从盒中一次摸出'2只球,如果这2只球的编号均能被3整除,则获一等奖,奖金10元,如果这2只球的编号均为偶数,则获二等奖,奖金2元,其他情况均不获奖.
(1)若某人参加摸球游戏一次获奖金x元,求x的分布列及期望;
(2)若某人摸一次且获奖,求他获得一等奖的概率.
(1)X的分布列为
期望EX=X 0 2 10 P(X) 


 ;(2)
;(2)
解析试题分析:(1)易知X的可能取值为0,2, 10,
X的分布列为
期望EX=X 0 2 10 P(X) 


 (元)………6分
(元)………6分
(2)设摸一次得一等奖为事件A,摸一次得二等奖为事件B,
则

某人摸一次且获奖为事件 ,显然A、B互斥 所以
,显然A、B互斥 所以
故某人摸一次且获奖,他获得一等奖的概率为: ………………12分
………………12分
考点:本题考查了随机事件的概率及期望的求法
点评:本题考查了随机事件的概率及随机变量的分布列、期望的综合运用,考查了学生的计算能力及解决实际问题的能力,掌握求分布列的步骤及期望公式是解决此类问题的关键

练习册系列答案
相关题目
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对楼市“楼市限购令”赞成人数如下表.
| 月收入(单位百元) | [15,25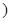 | [25,35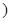 | [35,45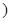 | [45,55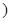 | [55,65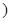 | [65,75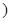 |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
| | 月收入不低于55百元的人数 | 月收入低于55百元的人数 | 合计 |
| 赞成 | 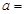 | 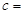 | |
| 不赞成 |  |  | |
| 合计 | | | |
 ,求随机变量
,求随机变量 的分布列及数学期望。
的分布列及数学期望。  道备选题中一次性随机抽取
道备选题中一次性随机抽取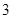 道题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中
道题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中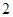 道题的便可通过.已知
道题的便可通过.已知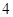 道题能正确完成,
道题能正确完成, ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响. (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和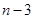 个白球.已知从
个白球.已知从 ,且
,且 。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于
。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于 。
。 为第一次取到白球时的取球次数,求
为第一次取到白球时的取球次数,求 。
。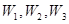 ,物理、化学、生物获得等级不是A的事件分别记为
,物理、化学、生物获得等级不是A的事件分别记为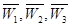 .
.
 的数学期望
的数学期望 .
.