题目内容
(本小题满分12分)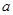 、
、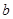 是常数,关于
是常数,关于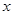 的一元二次方程
的一元二次方程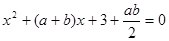 有实数解记为事件
有实数解记为事件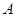 .
.
(1)若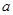 、
、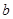 表示投掷两枚均匀骰子出现的点数,求
表示投掷两枚均匀骰子出现的点数,求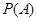 ;
;
(2)若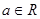 、
、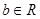 ,
,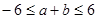 且
且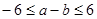 ,求
,求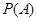 .
.
(1) (2)
(2)
解析试题分析:(1)方程有实数解, ,即
,即
依题意, 、
、 、
、 、
、 、
、 、
、 ,
, 、
、 、
、 、
、 、
、 、
、 ,
,
所以,“投掷两枚均匀骰子出现的点数”共有 种结果………………2分
种结果………………2分
当且仅当“ 且
且 、
、 、
、 ”,或“
”,或“ 且
且 、
、 ”,或“
”,或“ 且
且 ”时,
”时, 不成立
不成立
所以满足 的结果有
的结果有 种 ………………5分,
种 ………………5分,
从而 ………………6分.
………………6分.
(2)在平面直角坐标系 中,直线
中,直线 与
与 围成一个正方形
围成一个正方形
正方形边长即直线 与
与 之间的距离为
之间的距离为 …………8分
…………8分
正方形的面积
圆 的面积为
的面积为 ………………10分
………………10分
所以 ………………12分.
………………12分.
考点:古典概型概率与几何概型概率
点评:古典概型概率需找到所有基本事件种数与满足题意要求的基本事件种数,然后求其比值,几何概型概率一般找的是长度比面积比或体积比

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
为了参加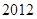 贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出
贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出 人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
| 班级 | 高三(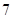 )班 )班 | 高三(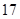 )班 )班 | 高二(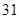 )班 )班 | 高二(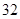 )班 )班 |
| 人数 | 12 | 6 | 9 | 9 |
(Ⅱ)该中学篮球队奋力拼搏,获得冠军.若要从高三年级抽出的队员中选出两位队员作为冠军的代表发言,求选出的两名队员来自同一班的概率.
(本小题满分12分)
甲,乙,丙三位学生独立地解同一道题,甲做对的概率为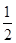 ,乙,丙做对的概率分别为
,乙,丙做对的概率分别为 ,
, (
( >
> ),且三位学生是否做对相互独立.记
),且三位学生是否做对相互独立.记 为这三位学生中做对该题的人数,其分布列为:
为这三位学生中做对该题的人数,其分布列为:
 | 0 | 1 | 2 | 3 |
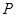 | 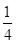 |  | 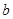 | 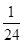 |
(2) 求
 ,
, 的值;
的值;(3) 求
 的数学期望.
的数学期望. 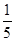 ,中奖后电信公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为X(元).
,中奖后电信公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为X(元). (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和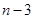 个白球.已知从
个白球.已知从 ,且
,且 。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于
。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于 。
。 为第一次取到白球时的取球次数,求
为第一次取到白球时的取球次数,求 。
。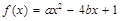 .
. 在区间
在区间 上是增函数的概率;
上是增函数的概率; 内的一点,求函数
内的一点,求函数