Question

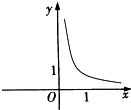定义域为{x|x≠0}的偶函数f（x）的部分图象如图所示，则在（-∞，0）上，下列函数中与f（x）的单调性不同的是（　　）

• A．y=log

  1

  2

  |x|
• B．y=x|x|
• C．y=x+

  1

  x

• D．y=

  2x ，     x≥0 -2-x，x＜0

Answer 1

分析：利用偶函数的性质，可知函数f（x）在（-∞，0）单调递增，然后根据函数特点进行判断即可．

解答：解：由图象可知函数f（x）在（0，+∞）上单调递减，
∵函数f（x）是偶函数，∴函数f（x）在（-∞，0）单调递增．
A．根据复合函数的单调性的性质可知，函数y=log

1

2

|x|在（-∞，0）单调递增．
B．y=x|x|=

x2， x≥0 -x2，x＜0

，则函数y=x|x|在（-∞，0）单调递增．
C．y'=1-

1

x2

=

x2-1

x2

，由y'＞0，解得x＞1或x＜-1，∴函数在（-∞，0）上不单调，与条件单调性不同．
D．当x＜0时，y=-2-x=-(

1

2

)x，为增函数．
故选：C..

点评：本题主要考查函数单调性和奇偶性的关系，要求熟练掌握常见函数的单调性．