题目内容
已知椭圆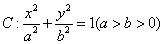 的离心率为
的离心率为 , 以原点为圆心、椭圆的短半轴长为半径的圆与直线
, 以原点为圆心、椭圆的短半轴长为半径的圆与直线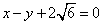 相切.
相切.
(Ⅰ)求椭圆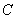 的方程;
的方程;
(Ⅱ)设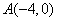 ,过点
,过点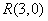 作与
作与 轴不重合的直线
轴不重合的直线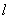 交椭圆于
交椭圆于 、
、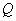 两点,连结
两点,连结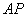 、
、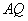 分别交直线
分别交直线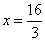 于
于 、
、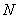 两点.试问直线
两点.试问直线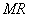 、
、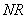 的斜率之积是否为定值,若是,求出该定值;若不是,请说明理由.
的斜率之积是否为定值,若是,求出该定值;若不是,请说明理由.
解(1)
 ,故
,故
(2)设 ,若直线
,若直线 与纵轴垂直,
与纵轴垂直,
则 中有一点与
中有一点与 重合,与题意不符,
重合,与题意不符,
故可设直线 .
.
将其与椭圆方程联立,消去 得:
得:

 7分
7分
由 三点共线可知,
三点共线可知, ,
, ,
,
同理可得

而
所以
故直线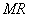 、
、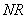 的斜率为定值
的斜率为定值 .
.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 ,则
,则 ”的否命题为:“若
”的否命题为:“若 ”.
”. ” 是“
” 是“ ”的必要不充分条件.
”的必要不充分条件. ,则
,则 ”的逆否命题为真命题.
”的逆否命题为真命题. R使得
R使得 ”的否定是:“
”的否定是:“ R均有
R均有 __________.
__________. 上的函数
上的函数 ,对任意
,对任意 ,都有
,都有
 函数”.给出下列函数:
函数”.给出下列函数: ;②
;② ;③
;③ ;④
;④ .
. B.
B. C.
C. D.
D.
 为极点、
为极点、 ,曲线
,曲线 (
( 为参数),则点
为参数),则点 ,则
,则 =( )
=( ) B.
B.  C.
C.  D.
D. 
 的值为6,那么运行相应程序,输出的
的值为6,那么运行相应程序,输出的 的值为( )
的值为( )
 共线,则有( )
共线,则有( )
 B
B C
C D
D