题目内容
9.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2 于 A,B 两点.若|$\overrightarrow{OA}$|,|$\overrightarrow{AB}$|,|$\overrightarrow{OB}$|成等差数列,且$\overrightarrow{BF}$与$\overrightarrow{FA}$反向,则该双曲线的离心率为( )| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\frac{5}{2}$ |
分析 设实轴长为2a,虚轴长为2b,令∠AOF=α,则由题意知tanα=$\frac{b}{a}$,△AOB中,∠AOB=180°-2α,tan∠AOB=-tan2α=$\frac{AB}{OA}$,由此推导出-tan2α=-$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{4}{3}$,从而能求出离心率.
解答 解:如图,设实轴长为2a,虚轴长为2b,
令∠AOF=α,则由题意知tanα=$\frac{b}{a}$,
△AOB中,∠AOB=180°-2α,tan∠AOB=-tan2α
=$\frac{AB}{OA}$,
∵|$\overrightarrow{OA}$|,|$\overrightarrow{AB}$|,|$\overrightarrow{OB}$|成等差数列,
∴设|$\overrightarrow{OA}$|=m-d、|$\overrightarrow{AB}$|=m、|$\overrightarrow{OB}$|=m+d,
∵OA⊥BF,∴(m-d)2+m2=(m+d)2,
整理,得d=$\frac{1}{4}$m,
∴-tan2α=-$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{4}{3}$
解得$\frac{b}{a}$=2或$\frac{b}{a}$=-$\frac{1}{2}$(舍),
∴b=2a,c=$\sqrt{5}$a,
∴e=$\frac{c}{a}$=$\sqrt{5}$.
故选C.
点评 本题考查双曲线的离心率的求法,考查等差数列的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
19.函数f(x)=sin2(x+$\frac{π}{4}$)-sin2(x-$\frac{π}{4}$)是( )
| A. | 最小正周期为2π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的偶函数 | D. | 最小正周期为π的奇函数 |
4.执行如图所示的程序框图,若输入的 x=2017,则输出的i=( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
1.设集合A={x|x<2},B={y|y=2x-1,x∈A},则A∩B=( )
| A. | (-∞,3) | B. | [2,3) | C. | (-∞,2) | D. | (-1,2) |
19.已知某三棱锥的三视图如图所示,则该三棱锥外接球的表面积是( )
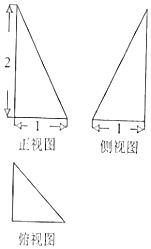

| A. | $\sqrt{6}π$ | B. | 6π | C. | 24π | D. | 36π |