题目内容
已知函数 ,其中a为正实数,e=2.718….
,其中a为正实数,e=2.718….
(I)若 是y=f(x)的一个极值点,求a的值;
是y=f(x)的一个极值点,求a的值;
(II)求f(x)的单调区间.
解:f′(x)=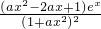 .
.
(I)因为x= 是函数y=f(x)的一个极值点,
是函数y=f(x)的一个极值点,
所以f′( )=0,
)=0,
因此 a-a+1=0,
a-a+1=0,
解得a= .
.
经检验,当a= 时,x=
时,x= 是y=f(x)的一个极值点,故所求a的值为
是y=f(x)的一个极值点,故所求a的值为 .…(4分)
.…(4分)
(II)f′(x)=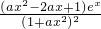 (a>0),
(a>0),
令f′(x)=0得ax2-2ax+1=0…①
(i)当△=(-2a)2-4a>0,即a>1时,方程①两根为
x1=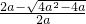 =
=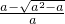 ,x2=
,x2=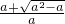 .
.
此时f′(x)与f(x)的变化情况如下表:
所以当a>1时,f(x)的单调递增区间为(-∞,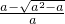 ),(
),(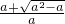 ,+∞); f(x)的单调递减区间为(
,+∞); f(x)的单调递减区间为(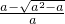 ,
,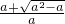 ).
).
(ii)当△=4a2-4a≤0时,即0<a≤1时,ax2-2ax+1≥0,
即f′(x)≥0,此时f(x)在(-∞,+∞)上单调递增.
所以当0<a≤1时,f(x)的单调递增区间为(-∞,+∞).…(13分)
分析:(I)依题意,由f′( )=0,即可求得a的值;
)=0,即可求得a的值;
(II)求f′(x)=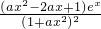 ,令f′(x)=0可求得方程ax2-2ax+1=0的根,将f′(x)与f(x)的变化情况列表,可求得f(x)的单调区间.
,令f′(x)=0可求得方程ax2-2ax+1=0的根,将f′(x)与f(x)的变化情况列表,可求得f(x)的单调区间.
点评:本题考查利用导数研究函数的极值,考查利用导数研究函数的单调性,求得f′(x)=0之后,将f′(x)与f(x)的变化情况列表是关键,属于中档题.
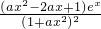 .
.(I)因为x=
 是函数y=f(x)的一个极值点,
是函数y=f(x)的一个极值点,所以f′(
 )=0,
)=0,因此
 a-a+1=0,
a-a+1=0,解得a=
 .
.经检验,当a=
 时,x=
时,x= 是y=f(x)的一个极值点,故所求a的值为
是y=f(x)的一个极值点,故所求a的值为 .…(4分)
.…(4分)(II)f′(x)=
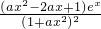 (a>0),
(a>0),令f′(x)=0得ax2-2ax+1=0…①
(i)当△=(-2a)2-4a>0,即a>1时,方程①两根为
x1=
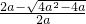 =
=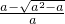 ,x2=
,x2=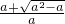 .
.此时f′(x)与f(x)的变化情况如下表:
| x | (-∞,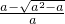 ) ) | 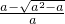 | (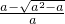 , ,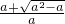 ) ) | 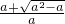 | (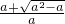 ,+∞) ,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
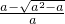 ),(
),(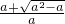 ,+∞); f(x)的单调递减区间为(
,+∞); f(x)的单调递减区间为(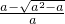 ,
,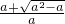 ).
).(ii)当△=4a2-4a≤0时,即0<a≤1时,ax2-2ax+1≥0,
即f′(x)≥0,此时f(x)在(-∞,+∞)上单调递增.
所以当0<a≤1时,f(x)的单调递增区间为(-∞,+∞).…(13分)
分析:(I)依题意,由f′(
 )=0,即可求得a的值;
)=0,即可求得a的值;(II)求f′(x)=
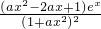 ,令f′(x)=0可求得方程ax2-2ax+1=0的根,将f′(x)与f(x)的变化情况列表,可求得f(x)的单调区间.
,令f′(x)=0可求得方程ax2-2ax+1=0的根,将f′(x)与f(x)的变化情况列表,可求得f(x)的单调区间.点评:本题考查利用导数研究函数的极值,考查利用导数研究函数的单调性,求得f′(x)=0之后,将f′(x)与f(x)的变化情况列表是关键,属于中档题.

练习册系列答案
相关题目
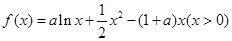 ,其中a为实数。
,其中a为实数。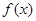 的单调区间;
的单调区间;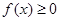 对定义域内的任意x恒成立,求实数a的取值范围。
对定义域内的任意x恒成立,求实数a的取值范围。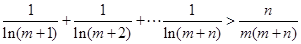 恒成立。
恒成立。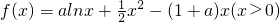 ,其中a为实数.
,其中a为实数. 恒成立.
恒成立. ,其中a为正实数,
,其中a为正实数, 是f(x)的一个极值点.
是f(x)的一个极值点. 时,求函数f(x)在[b,+∞)上的最小值.
时,求函数f(x)在[b,+∞)上的最小值. ,其中a为正实数,
,其中a为正实数, 是f(x)的一个极值点.
是f(x)的一个极值点. 时,求函数f(x)在[b,+∞)上的最小值.
时,求函数f(x)在[b,+∞)上的最小值.