题目内容
(14分)已知函数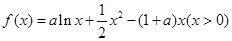 ,其中a为实数。
,其中a为实数。
(1)求函数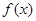 的单调区间;
的单调区间;
(2)若函数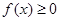 对定义域内的任意x恒成立,求实数a的取值范围。
对定义域内的任意x恒成立,求实数a的取值范围。
(3)证明,对于任意的正整数m,n,不等式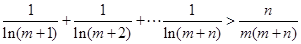 恒成立。
恒成立。
【答案】
(1)当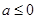 时,
时,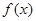 在
在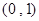 上递减,在
上递减,在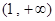 上递增
上递增
当 时,
时,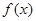 在
在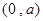 ,
,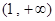 上递增,在
上递增,在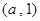 上递减
上递减
当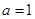 时,
时,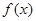 在
在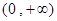 上递增
上递增
当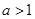 时,
时,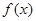 在
在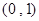 ,
,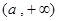 上递增,
上递增,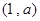 上递减;
上递减;
(2)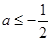 ;
;
(3)见解析。
【解析】本试题主要是考查了导数在研究函数中的运用。
(1)因为函数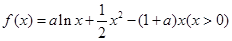 ,故
,故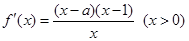 ,然手对于参数a进行分类讨论得到单调性。
,然手对于参数a进行分类讨论得到单调性。
(2)由(1)知当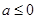 时
时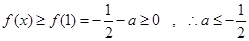
当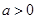 时,
时,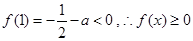 不恒成立
不恒成立
(3)由(2)知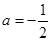 时,
时,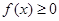 恒成立
恒成立
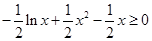
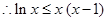 当且仅当
当且仅当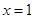 时以“=”
时以“=”
然后分析得到。
解:(1)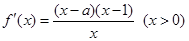
当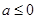 时,
时,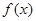 在
在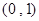 上递减,在
上递减,在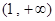 上递增
上递增
当 时,
时,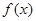 在
在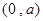 ,
,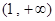 上递增,在
上递增,在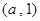 上递减
上递减
当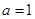 时,
时,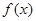 在
在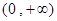 上递增
上递增
当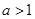 时,
时,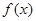 在
在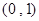 ,
,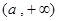 上递增,
上递增,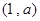 上递减 ……(5分)
上递减 ……(5分)
(2)由(1)知当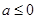 时
时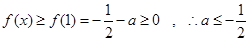
当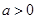 时,
时,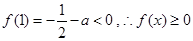 不恒成立
不恒成立
综上: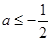 ……(9分)
……(9分)
(3)由(2)知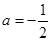 时,
时,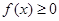 恒成立
恒成立
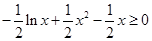
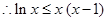 当且仅当
当且仅当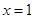 时以“=”
时以“=”
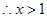 时,
时,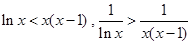
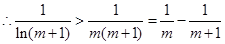
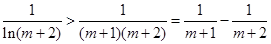
……
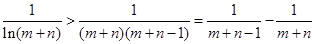
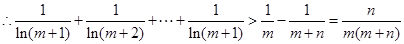 ……(14分)
……(14分)

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 已知函数
已知函数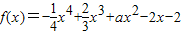 ,其中a为实常数,已知函数y=f(x)的图象在点(-1,f(-1))处的切线与y轴垂直.
,其中a为实常数,已知函数y=f(x)的图象在点(-1,f(-1))处的切线与y轴垂直.