题目内容
18. 如图,在底面为平行四边形的四棱锥P-ABCD中,PA⊥平面ABCD,且BC=2AB=4,∠ABC=60°,点E是PD的中点
如图,在底面为平行四边形的四棱锥P-ABCD中,PA⊥平面ABCD,且BC=2AB=4,∠ABC=60°,点E是PD的中点(Ⅰ)求证:AC⊥PB
(Ⅱ)若AP=2,求B到平面AEC的距离.
分析 (Ⅰ)由余弦定理求出AC=2$\sqrt{3}$,再由勾股定理得AC⊥AB,由线面垂直得AC⊥PA,从而AC⊥平面PAB,由此能证明AC⊥PB.
(Ⅱ)以A为原点,AC为x轴,AB为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出B到平面AEC的距离.
解答 证明:(Ⅰ)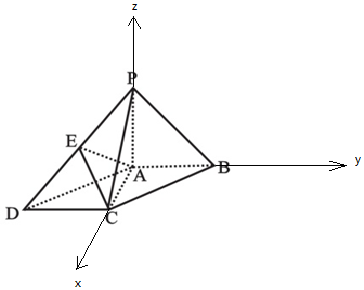 ∵BC=2AB=4,∠ABC=60°,
∵BC=2AB=4,∠ABC=60°,
∴AC=$\sqrt{4+16-2×2×4×cos60°}$=2$\sqrt{3}$,
∴AC2+AB2=BC2,∴AC⊥AB,
∵PA⊥平面ABCD,AC?平面ABCD,
∴AC⊥PA,
∵PA∩AB=A,∴AC⊥平面PAB,
∵PB?平面PAB,∴AC⊥PB.
解:(Ⅱ)以A为原点,AC为x轴,AB为y轴,AP为z轴,建立空间直角坐标系,
∵AP=2,E是PD的中点,
∴B(0,2,0),A(0,0,0),C(2$\sqrt{3}$,0,0),P(0,0,2),D(2$\sqrt{3}$,-2,0),E($\sqrt{3}$,-1,1),
$\overrightarrow{AE}$=($\sqrt{3},-1,1$),$\overrightarrow{AC}$=(2$\sqrt{3}$,0,0),$\overrightarrow{AB}$=(0,2,0),
设平面AEC的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AE}=\sqrt{3}x-y+z=0}\\{\overrightarrow{n}•\overrightarrow{AC}=2\sqrt{3}x=0}\end{array}\right.$,取y=1,得$\overrightarrow{n}$=(0,1,1),
∴B到平面AEC的距离:
d=$\frac{|\overrightarrow{n}•\overrightarrow{AB}|}{|\overrightarrow{n}|}$=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$.
点评 本题考查线线垂直的证明,考查点到平面的距离的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想、数形结合思想,是中档题.

 阅读快车系列答案
阅读快车系列答案| A. | DD1的中点 | B. | DD1的三等分点 | C. | D1C1的中点 | D. | A1D1的中点 |
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如图所示,则函数f(x)的解析式为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如图所示,则函数f(x)的解析式为( )| A. | f(x)=2sin($\frac{1}{2}$x+$\frac{π}{4}$) | B. | f(x)=4sin($\frac{1}{2}$x+$\frac{π}{4}$) | C. | f(x)=2sin($\frac{1}{2}$x+$\frac{3π}{4}$) | D. | f(x)=4sin($\frac{1}{2}$x+$\frac{3π}{4}$) |
 如图所示,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
如图所示,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.