题目内容
已知函数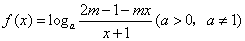 是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
(1)求实数m的值,并写出区间D;
(2)若底数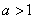 ,试判断函数
,试判断函数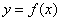 在定义域D内的单调性,并说明理由;
在定义域D内的单调性,并说明理由;
(3)当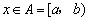 (
(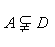 ,a是底数)时,函数值组成的集合为
,a是底数)时,函数值组成的集合为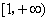 ,求实数
,求实数 的值.
的值.
(1)∵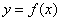 是奇函数,∴对任意
是奇函数,∴对任意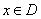 ,有
,有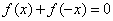 ,即
,即 .
.
化简此式,得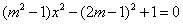 .又此方程有无穷多解(D是区间),必有
.又此方程有无穷多解(D是区间),必有
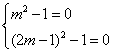 ,解得
,解得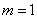 .∴
.∴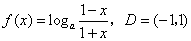 .
.
(2)当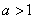 时,函数
时,函数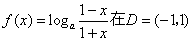 上是单调减函数.
上是单调减函数.
理由:令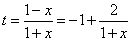 .
.
易知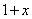 在
在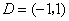 上是随
上是随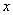 增大而增大,
增大而增大,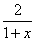 在
在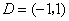 上是随
上是随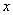 增大而减小,
增大而减小,
故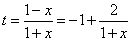 在
在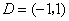 上是随
上是随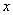 增大而减小.
增大而减小.
于是,当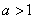 时,函数
时,函数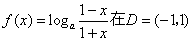 上是单调减函数
上是单调减函数
(3) ∵ ,∴
,∴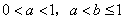 .
.
∴依据(2)的道理,当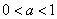 时,函数
时,函数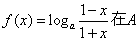 上是增函数,
上是增函数,
即 ,解得
,解得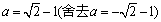 .
.
若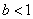 ,则
,则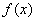 在A上的函数值组成的集合为
在A上的函数值组成的集合为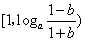 ,不满足函数值组成的集合是
,不满足函数值组成的集合是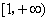 的要求.(也可利用函数的变化趋势分析,得出b=1)∴必有
的要求.(也可利用函数的变化趋势分析,得出b=1)∴必有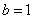 .
.
因此,所求实数 的值是
的值是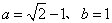 .
.

练习册系列答案
相关题目
 .
. PAB与
PAB与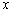 的方程
的方程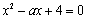 ,
,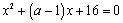 ,
,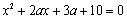 中,已知至少有一个方程有实数根,则实数
中,已知至少有一个方程有实数根,则实数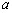 的取值范围为( )
的取值范围为( )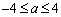 B.
B. 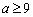 或
或 C.
C. 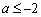 或
或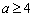 D.
D. 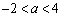
 三边的中点)得到的几何体如图2,则按图2所示方向侧视该几何体所呈现的平面图形为( )
三边的中点)得到的几何体如图2,则按图2所示方向侧视该几何体所呈现的平面图形为( )

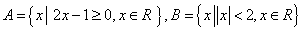 ,则
,则  =_________.
=_________.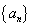 ,
,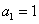 ,公比
,公比 ,若
,若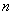 项和
项和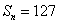 ,则
,则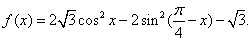 求函数
求函数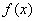 在区间
在区间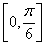 上的最大值.
上的最大值. 的定义域为
的定义域为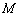 ,函数
,函数 的值域为
的值域为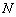 ,则
,则 .
.