题目内容
如图所示,在四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形.
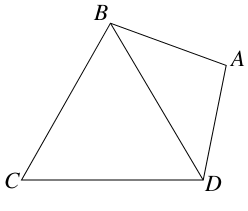
(1)将四边形ABCD的面积S表示为θ的函数;
(2)求S的最大值及此时θ角的值.

(1)将四边形ABCD的面积S表示为θ的函数;
(2)求S的最大值及此时θ角的值.
(1)S= +sin(θ-
+sin(θ- ),其中0<θ<π
),其中0<θ<π
(2)S取得最大值1+ ,此时θ=
,此时θ= +
+ =
=
 +sin(θ-
+sin(θ- ),其中0<θ<π
),其中0<θ<π(2)S取得最大值1+
 ,此时θ=
,此时θ= +
+ =
=
解:(1)S△ABD= ×1×1×sinθ=
×1×1×sinθ= sinθ,
sinθ,
因为△BDC是正三角形,则S△BDC= BD2.
BD2.
由△ABD及余弦定理,可知BD2=12+12-2×1×1×cosθ=2-2cosθ,
于是四边形ABCD的面积S= sinθ+
sinθ+ (2-2cosθ),
(2-2cosθ),
即S= +sin(θ-
+sin(θ- ),其中0<θ<π.
),其中0<θ<π.
(2)由(1),知S= +sin(θ-
+sin(θ- ),
),
由0<θ<π,得- <θ-
<θ- <
< ,
,
故当θ- =
= 时,S取得最大值1+
时,S取得最大值1+ ,此时θ=
,此时θ= +
+ =
= .
.
 ×1×1×sinθ=
×1×1×sinθ= sinθ,
sinθ,因为△BDC是正三角形,则S△BDC=
 BD2.
BD2.由△ABD及余弦定理,可知BD2=12+12-2×1×1×cosθ=2-2cosθ,
于是四边形ABCD的面积S=
 sinθ+
sinθ+ (2-2cosθ),
(2-2cosθ),即S=
 +sin(θ-
+sin(θ- ),其中0<θ<π.
),其中0<θ<π.(2)由(1),知S=
 +sin(θ-
+sin(θ- ),
),由0<θ<π,得-
 <θ-
<θ- <
< ,
,故当θ-
 =
= 时,S取得最大值1+
时,S取得最大值1+ ,此时θ=
,此时θ= +
+ =
= .
.
练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
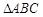 中,内角
中,内角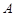 、
、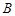 、
、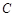 所对的边分别为
所对的边分别为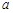 、
、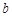 、
、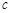 ,给出下列命题:①若
,给出下列命题:①若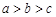 ,则
,则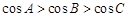 ;
;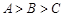 ,则
,则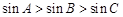 ;
;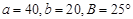 ,则
,则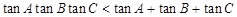 成立.
成立. 的气球
的气球 上测量铁桥
上测量铁桥 的长,如果测得桥头
的长,如果测得桥头 的俯角是
的俯角是 ,桥头
,桥头 的俯角是
的俯角是 ,则该桥的长可表示为
,则该桥的长可表示为




 ,
, 满足
满足 ,
, ,且对任意实数
,且对任意实数 ,不等式
,不等式 恒成立,设
恒成立,设 ,则
,则 ( )
( )



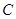 、
、 是两个小区所在地,
是两个小区所在地, 的垂直距离分别为
的垂直距离分别为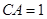
 ,
,

 ,在
,在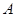 、
、 、
、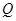 ,在
,在 处建造一个垃圾处理厂,使得
处建造一个垃圾处理厂,使得
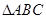 中,若
中,若 ,则
,则 中,A,B,C的对边分别为
中,A,B,C的对边分别为 ,且
,且 成等差数列,则B的大小为______________。
成等差数列,则B的大小为______________。 中,已知
中,已知 ,当
,当 时,
时,