题目内容
16. 如图AB为圆O直径,P为圆O外一点,过P点作PC⊥AB,垂足为C,PC交圆O于D点,PA交圆O于E点,BE交PC于F点
如图AB为圆O直径,P为圆O外一点,过P点作PC⊥AB,垂足为C,PC交圆O于D点,PA交圆O于E点,BE交PC于F点(Ⅰ)求证:∠PFE=∠PAB;
(Ⅱ)求证:CD2=CF•CP.
分析 (Ⅰ)在Rt△ACP中,∠PAC=90°-∠P;在Rt△PEF中,∠PFE=90°-∠P,即可证明:∠PFE=∠PAB;
(Ⅱ)证明△BCF∽△PCA,即可证明CD2=CF•CP.
解答 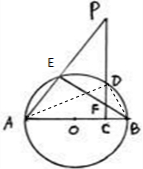 证明:(Ⅰ)AB为直径,E在圆O上,BE⊥AE
证明:(Ⅰ)AB为直径,E在圆O上,BE⊥AE
∵PC⊥AB,
∴∠PAC=90°-∠P,∠PFE=90°-∠P,
∴∠PAB=∠PFE-----------(5分)
(Ⅱ)连结AD、BD则AD⊥BD Rt△ABD中 CD2=AC•CB
由(Ⅰ)得△BCF∽△PCA,∴$\frac{BC}{PC}=\frac{CF}{AC}$,
∴CD2=BC•AC=CF•CP,
∴CD2=CF•CP-----------(10分)
点评 本题考查与圆有关的比例线段,考查三角形相似的判定,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 某圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为$\frac{π}{3}$的扇形,则该几何体的体积为2π.
某圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为$\frac{π}{3}$的扇形,则该几何体的体积为2π.