题目内容
在 中,角
中,角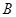 为锐角,已知内角
为锐角,已知内角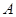 、
、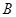 、
、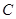 所对的边分别为
所对的边分别为 、
、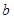 、
、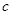 ,向量
,向量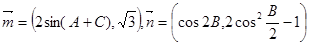 且向量
且向量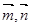 共线.
共线.
(1)求角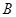 的大小;
的大小;
(2)如果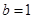 ,且
,且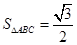 ,求
,求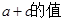 .
.
(1)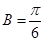 ,(2)
,(2)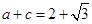
解析试题分析:(1)由向量共线关系得到一个等量关系: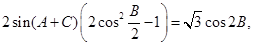 利用二倍角公式化简得:
利用二倍角公式化简得: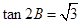 ,又
,又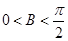 ,所以
,所以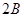 =
=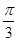 ,即
,即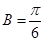 (2)结合(1),本题就是已知角B,所以三角形面积公式选用含B角,即
(2)结合(1),本题就是已知角B,所以三角形面积公式选用含B角,即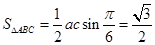 ,所以
,所以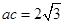 ,再结合余弦定理得:
,再结合余弦定理得: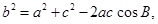
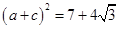 ,
,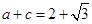 .应用余弦定理时,要注意代数变形,即
.应用余弦定理时,要注意代数变形,即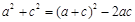 ,这样只需整体求解即可.
,这样只需整体求解即可.
试题解析:(1)由向量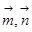 共线有:
共线有: 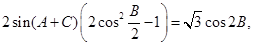
即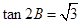 , 5分
, 5分
又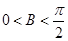 ,所以
,所以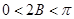 ,则
,则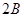 =
=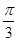 ,即
,即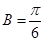 8分
8分
(2)由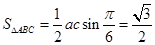 ,得
,得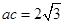 10分
10分
由余弦定理得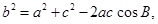
得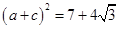 15分
15分
故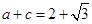 16分
16分
考点:向量共线,余弦定理

练习册系列答案
相关题目
A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.
(1)求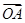 ·
·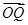 +S的最大值;
+S的最大值;
(2)若CB∥OP,求sin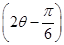 的值.
的值.
已知数列{an}满足a1=1,an+1= ,则其前6项之和是( )
,则其前6项之和是( )
| A.16 | B.20 | C.33 | D.120 |
 中,
中,  ,
, ,
, ,则
,则
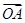 =(3,-4),
=(3,-4), =(6,-3),
=(6,-3), =(5-m,-3-m).
=(5-m,-3-m). ,-1),b=
,-1),b=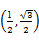 .
. ,
,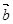 ,
,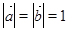 ,且
,且 ,其中
,其中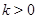
 ,求
,求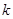 的值;
的值;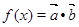 ,是否存在实数
,是否存在实数 ,使得
,使得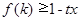 对任意的
对任意的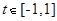 恒成立?若存在,求出实数
恒成立?若存在,求出实数 对应的复数为1+2i,向量
对应的复数为1+2i,向量 对应的复数为3-i.
对应的复数为3-i.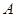 、
、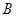 、
、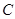 在一条直线上,
在一条直线上,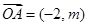 ,
,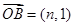 ,
,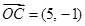 ,且
,且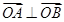 ,其中
,其中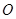 为坐标原点.
为坐标原点.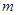 ,
,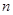 的值;
的值;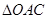 的重心为
的重心为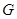 ,若存在实数
,若存在实数 ,使
,使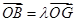 ,试求
,试求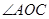 的大小.
的大小.