题目内容
20.已知函数f(x)=|x+1|+|x-1|.(Ⅰ)判断并证明函数f(x)的奇偶性;
(Ⅱ)作出函数f(x)的图象,并求其单调减区间.
分析 (Ⅰ)显然f(x)定义域为R,并可求出f(-x)=f(x),从而得出f(x)为偶函数;
(Ⅱ)去绝对值号得到$f(x)=\left\{\begin{array}{l}{-2x}&{x≤-1}\\{2}&{-1<x<1}\\{2x}&{x≥1}\end{array}\right.$,从而可画出f(x)的图象,根据图象便可得出f(x)的单调递减区间.
解答 解:(Ⅰ)f(x)的定义域为R;
∵f(-x)=|-x+1|+|-x-1|=|x-1|+|x+1|=f(x);
∴f(x)为偶函数;
(Ⅱ)$f(x)=|x+1|+|x-1|=\left\{\begin{array}{l}{-2x}&{x≤-1}\\{2}&{-1<x<1}\\{2x}&{x≥1}\end{array}\right.$;
图象如下所示: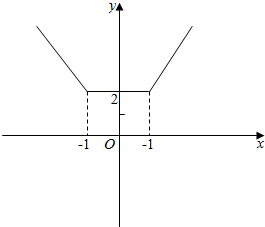
由图象可看出f(x)的单调减区间为:(-∞,-1].
点评 考查函数奇偶性的定义及其判断方法和过程,含绝对值函数的处理方法:去绝对值号,根据函数图象求函数单调减区间的方法.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
10.函数$y=sin({2x+\frac{π}{3}})$图象的对称中心可能是( )
| A. | $({-\frac{π}{6},0})$ | B. | $({-\frac{π}{12},0})$ | C. | $({\frac{π}{6},0})$ | D. | $({\frac{π}{12},0})$ |
11.设全集U={1,2,3,4},M={1,3,4},N={2,4},P={2},那么下列关系正确的是( )
| A. | P=(∁UM)∩N | B. | P=M∪N | C. | P=M∩(∁UN) | D. | P=M∩N |
5.设集合M={x|x≤$\sqrt{17}$},a=4$\sqrt{2}$,则( )
| A. | a∈M | B. | a∉M | C. | a⊆M | D. | a>M |