题目内容
19.(Ⅰ)求值:sin270°-3cos180°-2tan135°-4cos300°;(Ⅱ) 已知α是第二象限的角,且sinα=$\frac{5}{13}$,求cos(π+α)cos(α-$\frac{π}{2}$)+cos($\frac{3π}{2}$+α)•sin(π-α)的值.
分析 (Ⅰ)利用特殊角的三角函数值,诱导公式化简已知即可计算得解.
(Ⅱ) 由已知利用同角三角函数基本关系式可求cosα,利用诱导公式化简所求即可计算得解.
解答 解:(Ⅰ)sin270°-3cos180°-2tan135°-4cos300°
=(-1)-3×(-1)-2×(-1)-4×$\frac{1}{2}$
=2;
(Ⅱ)∵α是第二象限的角,且sinα=$\frac{5}{13}$,可得:cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{12}{13}$,
∴cos(π+α)cos(α-$\frac{π}{2}$)+cos($\frac{3π}{2}$+α)•sin(π-α)
=(-cosα)sinα+sin2α
=sin2α-cosαsinα
=($\frac{5}{13}$)2-$\frac{5}{13}$×(-$\frac{12}{13}$)
=$\frac{85}{169}$.
点评 本题主要考查了诱导公式,特殊角的三角函数值,同角三角函数基本关系式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
9.已知f(x)=ex(sinx-cosx),则函数f(x)的图象x=$\frac{π}{2}$处的切线的斜率为( )
| A. | 2e | B. | ${e^{\frac{π}{2}}}$ | C. | e | D. | 2${e^{\frac{π}{2}}}$ |
10.在六条棱长均相等的三棱锥A-BCD中,已知M,N,K分别是棱AB,CD,AC的中点,则下列结论中:
①MN∥AD;②NK∥平面ABD;③AB⊥CD;④平面CDM⊥平面ABN,正确的个数有( )
①MN∥AD;②NK∥平面ABD;③AB⊥CD;④平面CDM⊥平面ABN,正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.已知tanα<0,|cosα|=cosα,则α是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
4.执行如图所示的程序框图,如果输入的N=2016,那么输出的S=( )
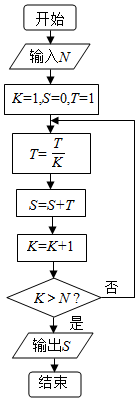

| A. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2015}$ | B. | 1+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{2015!}$ | ||
| C. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2016}$ | D. | 1+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{2016!}$ |
8.已知抛物线y2=2px(p>0)与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的交点为A,B,且直线AB,过两曲线的公共焦点F,则双曲线的离心率为e( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$+1 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{2}$+2 |
9.已知a=1,b,c∈{1,2,4},则以a,b,c为长度的三条线段能构成三角形的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{10}{27}$ | C. | $\frac{4}{9}$ | D. | $\frac{2}{3}$ |
