题目内容
过点(－5，－4)作一直线l，使它与两坐标轴相交且与两轴所围成的三角形面积为5个平方单位，求直线l的方程.
解:设直线l的方程为
=1(a≠0，b≠0).∵直线l经过点(－5，－4),
∴
＋
=1，即－5b－
又直线l与两坐标轴围成的三角形面积为5,
∴
|a|·|b|=5，即ab=±10.
解方程组
得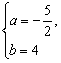
或
故所求直线l的方程是8x－5y＋20=0或2x－5y－10=0.
点评:此题中直线l满足两个条件：(1)过点(－5，－4);(2)与坐标轴围成的三角形面积为5.所以要求直线l的方程，有两条路可走，一是用直线方程的点斜式求k，二是用直线方程的截距式求a、b.第二条路解题过程较为简便，所以此例选择了此法.
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
过点P（1，2）作直线l，使直线l与点M（2，3）和点N（4，-5）距离相等，则直线l的方程为（ ）
| A、y+2=-4（x+1） | B、3x+2y-7=0或4x+y-6=0 | C、y-2=-4（x-1） | D、3x+2y-7=0或4x+y+6=0 |