题目内容
13.已知角θ的终边经过点P(-1,-$\sqrt{2}$).则sin2θ+sin(3π-θ)cos(2π+θ)-$\sqrt{2}$cos2θ=( )| A. | -$\frac{\sqrt{2}}{6}$ | B. | $\frac{\sqrt{2}}{6}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
分析 根据角α的终边经过点P(-1,-$\sqrt{2}$),可知到原点的距离r=$\sqrt{(-1)^{2}+(-\sqrt{2})^{2}}$=$\sqrt{3}$,得到sinα和cosα的值,利用诱导公式化简所求,然后把sinα和cosα代入即可求出值.
解答 解:∵角a的终边经过点P(-1,-$\sqrt{2}$).
∴r=3,sinα=$\frac{y}{r}$=-$\frac{\sqrt{6}}{3}$,cosα=$\frac{x}{r}$=-$\frac{\sqrt{3}}{3}$,
∴sin2θ+sin(3π-θ)cos(2π+θ)-$\sqrt{2}$cos2θ
=sin2θ+sinθcosθ-$\sqrt{2}$cos2θ
=(-$\frac{\sqrt{6}}{3}$)2+(-$\frac{\sqrt{6}}{3}$)(-$\frac{\sqrt{3}}{3}$)-$\sqrt{2}×$(-$\frac{\sqrt{3}}{3}$)2
=$\frac{2}{3}$.
故选:D.
点评 本题主要考查学生会根据终边经过的点求出所对应的三角函数值,灵活运用诱导公式化简求值.学生做题的思路是将原式化为关于sinα和cosα的式子,属于基础题.

练习册系列答案
相关题目
3.在平行四边形ABCD中,E为BC的中点,设$\overrightarrow{AC}$=m$\overrightarrow{AE}$+n$\overrightarrow{AD}$,则m+n=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
11.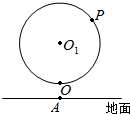 如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面1米,点O在地面上的射影为A.风车圆周上一点M从最低点O开始,逆时针方向旋转40秒后到达P点,则点P到点A的距离与点P的高度之和为( )
如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面1米,点O在地面上的射影为A.风车圆周上一点M从最低点O开始,逆时针方向旋转40秒后到达P点,则点P到点A的距离与点P的高度之和为( )
 如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面1米,点O在地面上的射影为A.风车圆周上一点M从最低点O开始,逆时针方向旋转40秒后到达P点,则点P到点A的距离与点P的高度之和为( )
如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面1米,点O在地面上的射影为A.风车圆周上一点M从最低点O开始,逆时针方向旋转40秒后到达P点,则点P到点A的距离与点P的高度之和为( )| A. | 5 | B. | 4$+\sqrt{7}$ | C. | 4$+\sqrt{17}$ | D. | 4$+\sqrt{19}$ |
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,CA=CB=CC1=1,则直线A1B与平面BB1C1C所成角的正弦值为$\frac{\sqrt{3}}{3}$.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,CA=CB=CC1=1,则直线A1B与平面BB1C1C所成角的正弦值为$\frac{\sqrt{3}}{3}$.