题目内容
已知曲线C：y=-x2+x+2关于点M（a，2a）对称的曲线为Cn，且曲线C与Cn有两个不同的交点A、B，设直线AB的斜率为k，求k的取值范围．
分析：设出曲线Cn上的任一点，利用对称性找出该点关于M的对称点，代入曲线C后整理即可得到曲线Cn的方程，
两曲线方程联立后由判别式大于0得到a的取值范围，由根与系数关系得到两个交点的横坐标的和与积，把纵坐标用横坐标表示后作差，整理后得到两点连线的斜率（用a表示），根据a的范围可得直线AB的斜率范围．
两曲线方程联立后由判别式大于0得到a的取值范围，由根与系数关系得到两个交点的横坐标的和与积，把纵坐标用横坐标表示后作差，整理后得到两点连线的斜率（用a表示），根据a的范围可得直线AB的斜率范围．
解答：解：设（x，y）为曲线Cn上的任一点，
（x，y）关于点M（a，2a）的对称点为（x0，y0），则x0=2a-x，y0=4a-y
依题意，点（x0，y0）在曲线C上∴4a-y=-（2a-x）2+2a-x+2
化简整理，得曲线Cn的方程：y=x2-（4a-1）x+4a2+2a-2
由方程组
消去y，整理得：x2-2ax+2a2+a-2=0（*）
设A（x1，y1），B（x2，y2），
则x1+x2=2a，x1x2=2a2+a-2
∵y1=-
+x1+2，y2=-
+x2+2
两式相减，得：
因曲线C与Cn交于不同两点，方程*应有两不等实根，∴△=4a2-4（2a2+a-2）＞0
即a2+a-2＜0
解之，得：-2＜a＜1，-1＜1-2a＜5
即AB的斜率k的取值范围是-1＜k＜5．
（x，y）关于点M（a，2a）的对称点为（x0，y0），则x0=2a-x，y0=4a-y
依题意，点（x0，y0）在曲线C上∴4a-y=-（2a-x）2+2a-x+2
化简整理，得曲线Cn的方程：y=x2-（4a-1）x+4a2+2a-2
由方程组
|
消去y，整理得：x2-2ax+2a2+a-2=0（*）
设A（x1，y1），B（x2，y2），
则x1+x2=2a，x1x2=2a2+a-2
∵y1=-
| x | 2 1 |
| x | 2 2 |
两式相减，得：
|
因曲线C与Cn交于不同两点，方程*应有两不等实根，∴△=4a2-4（2a2+a-2）＞0
即a2+a-2＜0
解之，得：-2＜a＜1，-1＜1-2a＜5
即AB的斜率k的取值范围是-1＜k＜5．
点评：本题考查了直线与圆锥曲线的综合题，考查了利用代入法求曲线的方程，训练了点差法求直线的斜率，考查了学生灵活处理和解决问题的能力，是有一定难度题目．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知曲线C：y=
(x＞0)及两点A1（x1，0）和A2（x2，0），其中x2＞x1＞0．过A1，A2分别作x轴的垂线，交曲线C于B1，B2两点，直线B1B2与x轴交于点A3（x3，0），那么（ ）
| 1 |
| x |
A、x1，
| ||
B、x1，
| ||
| C、x1，x3，x2成等差数列 | ||
| D、x1，x3，x2成等比数列 |
已知曲线C：y=
x3-x2-4x+1，直线l：x+y+2k-1=0，当x∈[-3，3]时，直线l 恒在曲线C的上方，则实数k的取值范围是（ ）
| 1 |
| 3 |
A、k＞-
| ||
B、k＜-
| ||
C、K＜
| ||
D、K＞
|
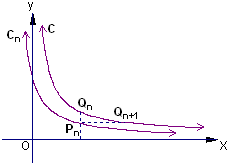如图，已知曲线C：