题目内容
1.已知抛物线$\left\{\begin{array}{l}{x=4{t}^{2}}\\{y=4t}\end{array}\right.$(t为参数),过其焦点F的直线l与抛物线分别交于A、B两点(A在第一象限内),|AF|=3|FB|,过AB的中点且垂于l的直线与x轴交于点G,则△ABG的面积为$\frac{32\sqrt{3}}{9}$.分析 抛物线$\left\{\begin{array}{l}{x=4{t}^{2}}\\{y=4t}\end{array}\right.$(t为参数),消去参数化为:y2=4x.设直线l的方程为:y=k(x-1),A(x1,y1),B(x2,y2).与抛物线方程联立化为:k2x2-(4+2k2)x+k2=0,利用根与系数的关系及其中点坐标公式可得线段AB的中点M$(1+\frac{2}{{k}^{2}},\frac{2}{k})$.由|AF|=3|FB|,可得$\overrightarrow{AF}$=3$\overrightarrow{FB}$,与根与系数的关系联立可得:k2=3,取k=$\sqrt{3}$.M$(\frac{5}{3},\frac{2}{\sqrt{3}})$,过AB的中点且垂于l的直线方程为:y-$\frac{2}{\sqrt{3}}$=-$\frac{1}{\sqrt{3}}$(x-$\frac{5}{3}$),可得G$(\frac{11}{3},0)$,求出点G到直线l的距离d.|AB|=$2\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$可得△ABG的面积S=$\frac{1}{2}$•d•|AB|.
解答 解:抛物线$\left\{\begin{array}{l}{x=4{t}^{2}}\\{y=4t}\end{array}\right.$(t为参数),消去参数化为:y2=4x.
设直线l的方程为:y=k(x-1),A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{y=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,化为:k2x2-(4+2k2)x+k2=0,
△>0,
∴x1+x2=$2+\frac{4}{{k}^{2}}$,x1x2=1,(*)
可得线段AB的中点M$(1+\frac{2}{{k}^{2}},\frac{2}{k})$.
∵|AF|=3|FB|,∴$\overrightarrow{AF}$=3$\overrightarrow{FB}$,
∴1-x1=3(x2-1),
与(*)联立可得:k2=3,取k=$\sqrt{3}$.
∴M$(\frac{5}{3},\frac{2}{\sqrt{3}})$,
∴过AB的中点且垂于l的直线方程为:y-$\frac{2}{\sqrt{3}}$=-$\frac{1}{\sqrt{3}}$(x-$\frac{5}{3}$),
令y=0,可得G$(\frac{11}{3},0)$,
∴点G到直线l的距离d=$\frac{|\sqrt{3}×\frac{11}{3}-0-\sqrt{3}|}{2}$=$\frac{4\sqrt{3}}{3}$.
|AB|=$2\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$2\sqrt{(2+\frac{4}{3})^{2}-4}$=$\frac{16}{3}$.
∴△ABG的面积S=$\frac{1}{2}$•d•|AB|=$\frac{1}{2}×$$\frac{4\sqrt{3}}{3}$×$\frac{16}{3}$=$\frac{32\sqrt{3}}{9}$.
故答案为:$\frac{32\sqrt{3}}{9}$.
点评 本题考查了抛物线的参数方程、直线与抛物线相交弦长问题、点到直线的距离公式、一元二次方程的根与系数的关系、中点坐标公式,考查了推理能力与计算能力,属于难题.

| A. | d>$\frac{8}{3}$ | B. | d<3 | C. | $\frac{8}{3}$≤d<3 | D. | $\frac{4}{3}$<d≤$\frac{3}{2}$ |
| A. | -2 | B. | $\frac{1}{2}$ | C. | 2 | D. | -$\frac{1}{2}$ |
| A. | $\frac{17}{15}$ | B. | $\frac{11}{15}$ | C. | $\frac{5}{3}$ | D. | $\frac{64}{15}$ |
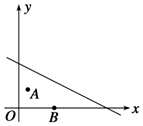 如图所示,某县相邻两镇在一平面直角坐标系下的坐标为A(1,2),B(4,0),一条河所在的直线方程为l:x+2y-10=0,若在河边l上建一座供水站P,使之到A,B两镇的管道最省,那么供水站P应建在什么地方?
如图所示,某县相邻两镇在一平面直角坐标系下的坐标为A(1,2),B(4,0),一条河所在的直线方程为l:x+2y-10=0,若在河边l上建一座供水站P,使之到A,B两镇的管道最省,那么供水站P应建在什么地方? 如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点.
如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点.