题目内容
一个球与正四面体的六条棱都相切,若正四面体的棱长为a,则这个球的体积是________.

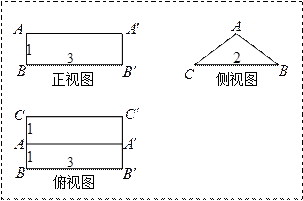
如图,

设球心为O,半径为r,体积为V,面BCD的中心为O1,棱BC的中心点为E,则 AO1= =
= =
= ,由 OB
,由 OB =O1O
=O1O +O1B
+O1B =
= +O1B
+O1B 得
得

 OB+
OB+ 故 OB=
故 OB=
于是 r =" OE" = =
=
 =
=
V= r
r =
= =
= .
.

设球心为O,半径为r,体积为V,面BCD的中心为O1,棱BC的中心点为E,则 AO1=
 =
= =
= ,由 OB
,由 OB =O1O
=O1O +O1B
+O1B =
= +O1B
+O1B 得
得
 OB+
OB+ 故 OB=
故 OB=
于是 r =" OE" =
 =
=
 =
=
V=
 r
r =
= =
= .
.
练习册系列答案
相关题目
 6条 B.5条 C.4条 D.3条
6条 B.5条 C.4条 D.3条 面上四点P、A、B、C满足:PA、PB、PC两两垂直,PA=PB=PC=2,则球
面上四点P、A、B、C满足:PA、PB、PC两两垂直,PA=PB=PC=2,则球
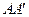 与
与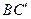 所成的角为
所成的角为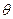 ,求
,求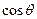 .
.
 ,则该半球的表面积是
,则该半球的表面积是 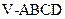 中,
中,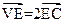 ,则三棱锥
,则三棱锥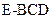 与几何体VABED的体积之比为 ( )
与几何体VABED的体积之比为 ( ) ,则它的表面积为________________.
,则它的表面积为________________.