题目内容
(本小题满分12分)已知数列 的前
的前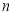 项和为
项和为 ,且
,且 ;数列
;数列 满足
满足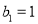 ,
,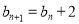 .
.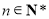 .
.
(Ⅰ)求数列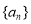 ,
, 的通项公式;
的通项公式;
(Ⅱ)记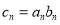 ,
,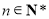 .求数列
.求数列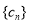 的前
的前 项和
项和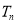 .
.
(Ⅰ) ;
; ;(Ⅱ)
;(Ⅱ)
【解析】
试题分析:(Ⅰ)先计算a1=2,然后利用变更序号法相减,可得an+1与an的递推关系,从而得出an的通项公式;{bn}是等差数列,可直接得到通项公式;(Ⅱ)根据anbn各自的性质,可知应该使用错位相减法即可求得Tn.
试题解析:(Ⅰ)∵ ?
?
当 时,
时, ?
?
? ?得,
?得, (
( ).
).
∵当 时,
时, ,且
,且 .
.
∴数列 是以
是以 为首项,公比为
为首项,公比为 的等比数列,
的等比数列,
∴数列 的通项公式为
的通项公式为 . 4分
. 4分
又由题意知, ,
, ,即
,即
∴数列 是首项为
是首项为 ,公差为
,公差为 的等差数列,
的等差数列,
∴数列 的通项公式为
的通项公式为 . 2分
. 2分
(Ⅱ)由(Ⅰ)知, 1分
1分
∴ ?
?
 ④
④
由? ④得
④得
 1分
1分

∴ 1分
1分
∴ 即
即
∴
∴数列 的前
的前 项和
项和 3分
3分
考点:等差数列,等比数列,通项公式,前n项和公式,错位相减法

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的导数为( )
的导数为( )



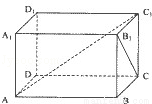
 = .
= . 中,内角
中,内角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
, .则边
.则边 的长度为__________..
的长度为__________.. 的方程
的方程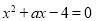 在区间
在区间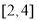 上有实数根,则实数
上有实数根,则实数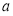 的取值范围是( )
的取值范围是( )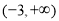 (B)
(B)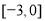 (C)
(C)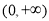 (D)
(D)
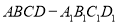 棱长为4,点
棱长为4,点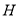 在棱
在棱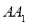 上,且
上,且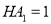 .在侧面
.在侧面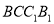 内作边长为1的正方形
内作边长为1的正方形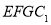 ,
,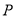 是侧面
是侧面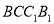 内一动点,且点
内一动点,且点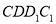 距离等于线段
距离等于线段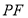 的长.则当点
的长.则当点 运动时,
运动时,  的最小值是 ( )
的最小值是 ( )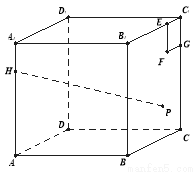
 (B)
(B)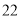 (C)
(C)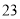 (D)
(D)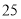
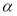 ,条件“直线l与平面α内的无数条直线都垂直”是“直线l与平面α垂直的( ).
,条件“直线l与平面α内的无数条直线都垂直”是“直线l与平面α垂直的( ).