题目内容
(本题满分13分)
一动圆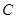 与圆
与圆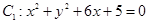 外切,同时与圆
外切,同时与圆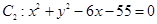 内切.
内切.
(1)求动圆圆心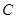 的轨迹
的轨迹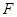 的方程;
的方程;
(2)在矩形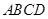 中(如图),
中(如图),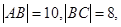
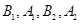 分别是矩形四边的中点,
分别是矩形四边的中点,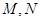 分别是
分别是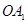 (其中
(其中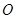 是坐标系原点)
是坐标系原点)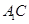 的中点,直线
的中点,直线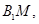
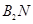 的交点为
的交点为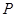 ,证明点
,证明点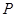 在轨迹
在轨迹 上.
上.
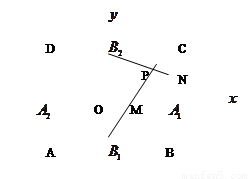
【答案】
(1) (
( )
)
(2)所以直线 的交点
的交点 在动圆圆心
在动圆圆心 的轨迹
的轨迹 上
上
【解析】解(1)设动圆 半径为
半径为 ,
,  ,
, 
 2分
2分



所以点 的轨迹是以
的轨迹是以 为焦点,长轴为10的椭圆
5分
为焦点,长轴为10的椭圆
5分
 ,所以点
,所以点 的轨迹
的轨迹 的方程是
的方程是 (
( )
7分
)
7分
(2) ,
8分
,
8分
 9分
9分
 解得
解得 即
即 11分
11分
将点 代入
代入 的方程得
的方程得 12分
12分
所以直线 的交点
的交点 在动圆圆心
在动圆圆心 的轨迹
的轨迹 上
13分
上
13分

练习册系列答案
相关题目
 ,
, ,
, .
.  ,
, ; (2) 若
; (2) 若 ,求
,求 的取值范围.
的取值范围. 的三个内角
的三个内角 依次成等差数列.
依次成等差数列. ,试判断
,试判断 ,求
,求
 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
. ,且
,且 ,
, ,求
,求 的值.
的值. 展开式中,求:
展开式中,求: 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD.
AD. ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.