题目内容
某企业某年生产某种产品,通过合理定价及促销活动,确保产销平衡(根据市场情况确定产量,使该年所生产产品刚好全部销售完毕),年产量、年销量均为x万件.已知每生产1万件产品需投入32万元的生产费用,另外该年生产设备折旧、维修等固定费用总共为4万元.每件产品定价为平均每件生产成本的150%进行销售,年销量x万件与年促销费用t万元之间满足关系: (k为常数),当年促销费用t=0万元时年销量是x=2万件.
(k为常数),当年促销费用t=0万元时年销量是x=2万件.
(Ⅰ)将年的利润y(万元)表示为促销费t(万元)的函数;
(Ⅱ)该企业年促销费投入多少万元时,企业年利润最大?相应年产量及最大年利润为多少?
注:生产成本=固定费用+生产费用 (不包括促销费用)
利润=销售收入-生产成本-促销费.
解:(Ⅰ)依题意,x=6- ,将t=0,x=2代入得k=4,
,将t=0,x=2代入得k=4,
∴年销售量x=6- ,t≥0.
,t≥0.
依题意,产销平衡即年产量等于年销量x万件,
∴当年生产量为x万件时,
年生产成本=32x+4=32(6- )+4=196-
)+4=196- ,
,
平均每件产品生产成本=(196- )÷x,
)÷x,
年销售收入=[(196- )÷x]×
)÷x]×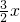 =
= ,
,
∴年利润y= -(196-
-(196- )-t=98-
)-t=98- -t,t≥0.
-t,t≥0.
(Ⅱ)∵y=98- =99-(t+1+
=99-(t+1+ ),t≥0
),t≥0
∴t+1+ ≥2
≥2 =16,
=16,
∴当且仅当t+1= ,即t=7时,ymax=99-16=83.
,即t=7时,ymax=99-16=83.
∴当促销费投入7万元时,企业年利润最大,
此时年产量x=5.5万件,年利润最大值为83万元.
分析:(Ⅰ)依题意,x=6- ,将t=0,x=2代入得k=4,年销售量x=6-
,将t=0,x=2代入得k=4,年销售量x=6- ,t≥0.产销平衡即年产量等于年销量x万件,由此分别求出年生产成本和年销售收入,由此能(将年的利润y(万元)表示为促销费t(万元)的函数.
,t≥0.产销平衡即年产量等于年销量x万件,由此分别求出年生产成本和年销售收入,由此能(将年的利润y(万元)表示为促销费t(万元)的函数.
(Ⅱ)由y=98- =99-(t+1+
=99-(t+1+ ),t≥0,利用均值不等式能求出当促销费投入7万元时,企业年利润最大,并能求出此时年产量和年利润最大值.
),t≥0,利用均值不等式能求出当促销费投入7万元时,企业年利润最大,并能求出此时年产量和年利润最大值.
点评:本题主要考查了函数模型的选择与应用,以及基本不等式在最值问题中的应用,同时考查了计算能力,属于难题.
 ,将t=0,x=2代入得k=4,
,将t=0,x=2代入得k=4,∴年销售量x=6-
 ,t≥0.
,t≥0.依题意,产销平衡即年产量等于年销量x万件,
∴当年生产量为x万件时,
年生产成本=32x+4=32(6-
 )+4=196-
)+4=196- ,
,平均每件产品生产成本=(196-
 )÷x,
)÷x,年销售收入=[(196-
 )÷x]×
)÷x]×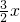 =
= ,
,∴年利润y=
 -(196-
-(196- )-t=98-
)-t=98- -t,t≥0.
-t,t≥0.(Ⅱ)∵y=98-
 =99-(t+1+
=99-(t+1+ ),t≥0
),t≥0∴t+1+
 ≥2
≥2 =16,
=16,∴当且仅当t+1=
 ,即t=7时,ymax=99-16=83.
,即t=7时,ymax=99-16=83.∴当促销费投入7万元时,企业年利润最大,
此时年产量x=5.5万件,年利润最大值为83万元.
分析:(Ⅰ)依题意,x=6-
 ,将t=0,x=2代入得k=4,年销售量x=6-
,将t=0,x=2代入得k=4,年销售量x=6- ,t≥0.产销平衡即年产量等于年销量x万件,由此分别求出年生产成本和年销售收入,由此能(将年的利润y(万元)表示为促销费t(万元)的函数.
,t≥0.产销平衡即年产量等于年销量x万件,由此分别求出年生产成本和年销售收入,由此能(将年的利润y(万元)表示为促销费t(万元)的函数.(Ⅱ)由y=98-
 =99-(t+1+
=99-(t+1+ ),t≥0,利用均值不等式能求出当促销费投入7万元时,企业年利润最大,并能求出此时年产量和年利润最大值.
),t≥0,利用均值不等式能求出当促销费投入7万元时,企业年利润最大,并能求出此时年产量和年利润最大值.点评:本题主要考查了函数模型的选择与应用,以及基本不等式在最值问题中的应用,同时考查了计算能力,属于难题.

练习册系列答案
相关题目