题目内容
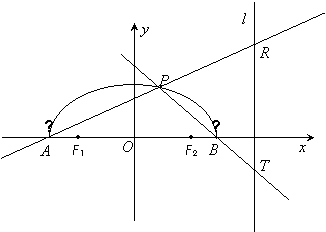
如图，在
轴上方有一段曲线弧
，其端点
、
在轴上（但不属于），对上任一点
及点
，
，满足：
．直线
，
分别交直线
于
，
两点．
（1）求曲线弧的方程；
（2）设，两点的纵坐标分别为
，求证：
；
（3）求
的最小值．
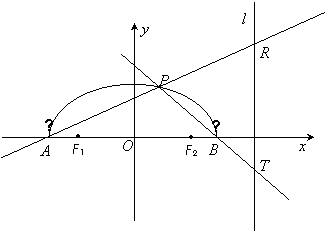
解：（1）由椭圆的定义，曲线是以，为焦点的半椭圆，
． ……………………………………………2分
∴的方程为
． ……………………………………………4分
（注：不写区间“
”扣1分）
（2）解法1：由（1）知，曲线的方程为，设
，
则有
， 即 
……① …………………………………6分
又
，
，从而直线
的方程为
AP：
； BP：
．………………7分
令
得，的纵坐标分别为
； 
.
∴ 
……② ………………………………………………………9分
将①代入②， 得 ． ………………………………………………10分
解法2：设
，则由
三点共线，得
…①
同理，由
三点共线得：
…② ……………………6分
由①×②得：
． …………………………………………………8分
由
，代入上式，
即． ……………………………………………………………………10分
（3）由（2）得：
当且仅当
，即
时，取等号． ………………………………13分
即的最小值是
． …………………………………………………………14分
练习册系列答案
相关题目
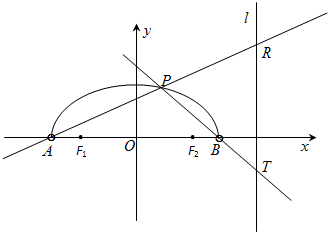如图，在x轴上方有一段曲线弧Γ，其端点A、B在x轴上（但不属于Γ），对Γ上任一点P及点F1（-1，0），F2（1，0），满足：
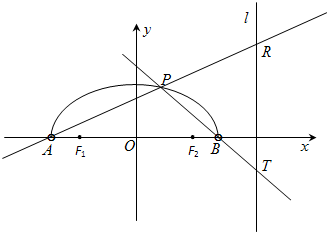如图，在x轴上方有一段曲线弧Γ，其端点A、B在x轴上（但不属于Γ），对Γ上任一点P及点F1（-1，0），F2（1，0），满足：
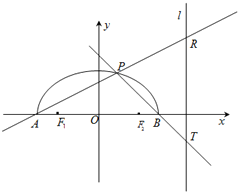如图，在x轴上方有一段曲线弧C，其端点A、B在x轴上（但不属于C），对C上任一点P及点F1（-1，0），F2（1，0），满足：
轴上方有一段曲线弧
，其端点
、
在
及点
，
，满足：
．直线
，
分别交直线
于
，
两点．
的最小值（用
表示）；
为正三角形？若存在，求