题目内容
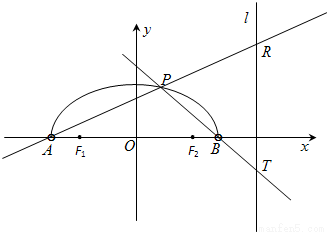
 如图,在x轴上方有一段曲线弧C,其端点A、B在x轴上(但不属于C),对C上任一点P及点F1(-1,0),F2(1,0),满足:|PF1|+|PF2|=2
如图,在x轴上方有一段曲线弧C,其端点A、B在x轴上(但不属于C),对C上任一点P及点F1(-1,0),F2(1,0),满足:|PF1|+|PF2|=2| 2 |
| 2 |
(Ⅰ)求曲线弧C的方程;
(Ⅱ)求|RT|的最小值(用a表示).
分析:( I)由题意知曲线弧C是以F1、F2为焦点的半椭圆,根据椭圆的定义写出椭圆的标准方程;
( II)设曲线C上的点P为(x0,y0),由点斜式写出直线AP,BP的方程,令x=a得R,T的纵坐标yR、yT;求|RT|=|yR-yT|的最小值即可.
( II)设曲线C上的点P为(x0,y0),由点斜式写出直线AP,BP的方程,令x=a得R,T的纵坐标yR、yT;求|RT|=|yR-yT|的最小值即可.
解答:解:( I)∵曲线弧C上任一点P满足:|PF1|+|PF2|=2
,
∴由椭圆的定义知,曲线C是以F1(-1,0),F2(1,0)为焦点的半椭圆,
且:c=1 , a=
, b2=a2-c2=1.
∴曲线弧C的方程为
+y2=1 (y>0).
(注:不写条件“y>0”应扣分)
( II)由(I)知,曲线C的方程为
+y2=1 (y>0),设P(x0,y0),
则有
+2
=2,即
=-
①;
又A(-
, 0),B(
, 0),从而直线AP,BP的方程为
AP:y=
(x+
); BP:y=
(x-
);
令x=a得R,T的纵坐标分别为yR=
(a+
); yT=
(a-
).
∴yR•yT=
(a2-2)②;
将①代入②,得 yRyT=
(2-a2).
∴|RT|=|yR-yT|=
≥
=
.
当且仅当|yR|=|yT|,即yR=-yT时,取等号.
即|RT|的最小值是
.
| 2 |
∴由椭圆的定义知,曲线C是以F1(-1,0),F2(1,0)为焦点的半椭圆,
且:c=1 , a=
| 2 |
∴曲线弧C的方程为
| x2 |
| 2 |
(注:不写条件“y>0”应扣分)
( II)由(I)知,曲线C的方程为
| x2 |
| 2 |
则有
| x | 2 0 |
| y | 2 0 |
| ||
|
| 1 |
| 2 |
又A(-
| 2 |
| 2 |
AP:y=
| y0 | ||
x0+
|
| 2 |
| y0 | ||
x0-
|
| 2 |
令x=a得R,T的纵坐标分别为yR=
| y0 | ||
x0+
|
| 2 |
| y0 | ||
x0-
|
| 2 |
∴yR•yT=
| ||
|
将①代入②,得 yRyT=
| 1 |
| 2 |
∴|RT|=|yR-yT|=
|
| 2|yRyT|-2yRyT |
| 2(a2-2) |
当且仅当|yR|=|yT|,即yR=-yT时,取等号.
即|RT|的最小值是
| 2(a2-2) |
点评:本题考查了椭圆的定义与标准方程以及直线与圆锥曲线的问题,是易错题.

练习册系列答案
相关题目
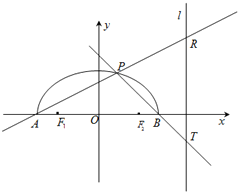
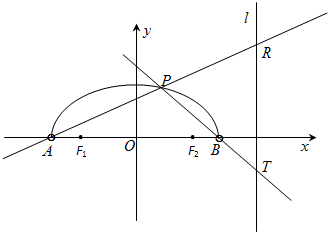 如图,在x轴上方有一段曲线弧Γ,其端点A、B在x轴上(但不属于Γ),对Γ上任一点P及点F1(-1,0),F2(1,0),满足:
如图,在x轴上方有一段曲线弧Γ,其端点A、B在x轴上(但不属于Γ),对Γ上任一点P及点F1(-1,0),F2(1,0),满足: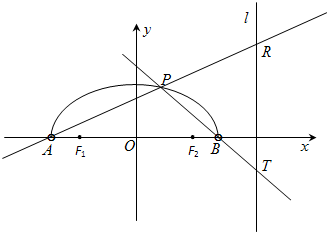 如图,在x轴上方有一段曲线弧Γ,其端点A、B在x轴上(但不属于Γ),对Γ上任一点P及点F1(-1,0),F2(1,0),满足:
如图,在x轴上方有一段曲线弧Γ,其端点A、B在x轴上(但不属于Γ),对Γ上任一点P及点F1(-1,0),F2(1,0),满足: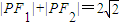 .直线AP,BP分别交直线
.直线AP,BP分别交直线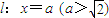 于R,T两点.
于R,T两点.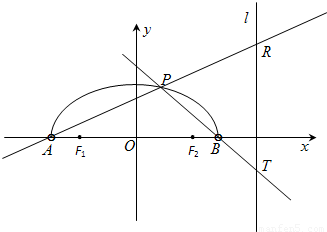
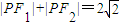 .直线AP,BP分别交直线
.直线AP,BP分别交直线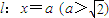 于R,T两点.
于R,T两点.