题目内容
如图所示的矩形ABCD中,BC=2AB,M是AD的中点,以BM为折痕将△ABM向上折起,使得平面ABM⊥平面BCDM.
(1)证明:AB⊥平面AMC;
(2)已知AB=2,求四棱锥A-BCDM的体积.

(1)证明:AB⊥平面AMC;
(2)已知AB=2,求四棱锥A-BCDM的体积.

考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:计算题,证明题,空间位置关系与距离
分析:(1)推CM⊥AB,AB⊥AM,证明AB⊥平面AMC;(2)梯形BCDM中解面积,高为AO,从而求出体积.
解答:
解:(1)证明:设AB=a,BC=2a,由题意BM=CM=
a;
则BM2+CM2=BC2,即BM⊥CM.
而平面ABM⊥平面BCDM,BM是平面ABM与平面BCDM的交线,
∴CM⊥平面ABM,AB⊆平面ABM
∴CM⊥AB,
∴CM⊥AB,又∵AB⊥AM
∴AB⊥平面AMC.
(2)在△BCM中,AB=AM=2,O为BM的中点
∴AO⊥BM,
平面ABM⊥平面BCDM,AO⊥平面BCDM,AO=
,
在梯形BCDM中,DM=CD=2,BC=4,S=
•6•2=6
VA-BCDM=
×S×AO=
×6×
=2
.
| 2 |
则BM2+CM2=BC2,即BM⊥CM.
而平面ABM⊥平面BCDM,BM是平面ABM与平面BCDM的交线,
∴CM⊥平面ABM,AB⊆平面ABM
∴CM⊥AB,
∴CM⊥AB,又∵AB⊥AM
∴AB⊥平面AMC.
(2)在△BCM中,AB=AM=2,O为BM的中点
∴AO⊥BM,
平面ABM⊥平面BCDM,AO⊥平面BCDM,AO=
| 2 |
在梯形BCDM中,DM=CD=2,BC=4,S=
| 1 |
| 2 |
VA-BCDM=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 2 |
点评:本题考查了线面垂直关系的证明,属于基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
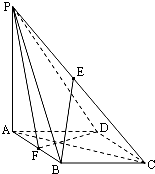 如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB中点.
如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB中点.