题目内容

8．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，右顶点为A，上顶点为B，以坐标原点O为圆心，椭圆C的短轴长为直径作圆O，截直线AB的弦长为$\frac{6\sqrt{7}}{7}$（a2-b2）．
（1）求椭圆C的标准方程；
（2）是否存在过椭圆C的右焦点F的直线l，与椭圆C相交于G、H两点，使得△AFG与△AFH的面积比为1：2？若存在，求出直线l的方程；若不存在，请说明理由．

分析 （1）直线AB的方程为：$\frac{x}{a}$+$\frac{y}{b}$=1，化为：bx-ay-ab=0，可得$\sqrt{{b}^{2}-（\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}）^{2}}$=$\frac{6\sqrt{7}}{7}$（a2-b2）．又$\frac{c}{a}$=$\frac{1}{2}$，a2=b2+c2．联立解出即可得出．
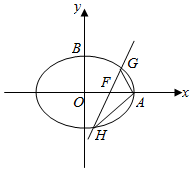
（2）如图所示，假设存在过椭圆C的右焦点F的直线l，与椭圆C相交于G、H两点，使得△AFG与△AFH的面积比为1：2．可得$\frac{|FG|}{|FH|}$=$\frac{1}{2}$．设直线FG的方程为：x=$\frac{1}{2}$+my．G（x1，y1），H（x2，y2）．与椭圆方程联立化为：（16+12m2）y2+12my-9=0．利用根与系数的关系及其$\frac{{y}_{1}}{-{y}_{2}}$=$\frac{1}{2}$．即可得出m．

解答 解：（1）直线AB的方程为：$\frac{x}{a}$+$\frac{y}{b}$=1，化为：bx-ay-ab=0，
则$\sqrt{{b}^{2}-（\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}）^{2}}$=$\frac{6\sqrt{7}}{7}$（a2-b2）．又$\frac{c}{a}$=$\frac{1}{2}$，a2=b2+c2．
联立解得：a=1，b=$\frac{\sqrt{3}}{2}$，c=$\frac{1}{2}$．
∴椭圆C的标准方程为${x}^{2}+\frac{4{y}^{2}}{3}$=1．
（2）如图所示，假设存在过椭圆C的右焦点F的直线l，
与椭圆C相交于G、H两点，使得△AFG与△AFH的面积比为1：2．
则$\frac{|FG|}{|FH|}$=$\frac{1}{2}$．
设直线FG的方程为：x=$\frac{1}{2}$+my．G（x1，y1），H（x2，y2）．
联立$\left\{\begin{array}{l}{x=\frac{1}{2}+my}\\{{x}^{2}+\frac{4{y}^{2}}{3}=1}\end{array}\right.$，化为：（16+12m2）y2+12my-9=0．
∴y1+y2=$\frac{-12m}{16+12{m}^{2}}$，y1y2=$\frac{-9}{16+12{m}^{2}}$．
$\frac{{y}_{1}}{-{y}_{2}}$=$\frac{1}{2}$．
化为：m2=$\frac{4}{5}$，解得m=$±\frac{2\sqrt{5}}{5}$．
因此存在过椭圆C的右焦点F的直线l：x=$\frac{1}{2}±\frac{2\sqrt{5}}{5}$y，
与椭圆C相交于G、H两点，使得△AFG与△AFH的面积比为1：2．

点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系，考查了数形结合思想方法、推理能力与计算能力，属于难题．

练习册系列答案
相关题目
18．如图1，平面五边形ABCFE是由边长为2的正方形ABCD与上底为1，高为$\sqrt{3}$的直角梯形组合而成，将五边形ABCFE沿着CD折叠，得到图2所示的空间几何体，其中AF⊥CF．
（Ⅰ）证明：BD⊥平面AFC；
（Ⅱ）求二面角A-FB-C的正弦值．
19．设|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=2，∠AOB=60°，$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$，且λ+μ=2（λ≥0，μ≥0），则$\overrightarrow{OA}$在$\overrightarrow{OP}$上的投影的取值范围是（0，$\frac{2\sqrt{3}}{3}$]．
16．三角形ABC是锐角三角形，若角θ终边上一点P的坐标为（sin A-cos B，cos A-sin B），则$\frac{sinθ}{|sinθ|}$+$\frac{cosθ}{|cosθ|}$+$\frac{tanθ}{|tanθ|}$的值是-1．
3．已知z=|$\frac{3+4i}{4-3i}$|+2i，则|z|$\overline{z}$+z|$\overline{z}$|=$2\sqrt{5}$．
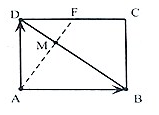13．如图，在矩形ABCD中，F是边CD的中点，M是AF与BD交点，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$
（1）用$\overrightarrow{a}$，$\overrightarrow{b}$表示向量$\overrightarrow{AF}$
（2）证明：M是对角线BD的三等分点．
20．甲、乙两人做定点投篮游戏，己知甲每次投篮命中率均为p，乙每次投篮命中的概率均为$\frac{1}{2}$，甲投篮3次均未命中的概率为$\frac{1}{27}$，甲、乙每次投篮是否命中相互之间没有影响．
（1）若甲投篮3次，求至少命中2次的概率；
（2）若甲、乙各投篮2次，设两人命中的总次数为X，求X的分布列和数学期望．
17．函数y=$\frac{1}{2}$-sin2x+$\sqrt{3}$sin xcosx的单调増区间为（　　）
A．[2kπ-$\frac{π}{6}$，2kπ+$\frac{5π}{6}$]（k∈Z）B．[2kπ-$\frac{π}{3}$，2kπ+$\frac{2π}{3}$]（k∈Z）
C．[kπ-$\frac{π}{6}$，kπ+$\frac{π}{3}$]（k∈Z）D．[kπ-$\frac{π}{3}$，2kπ+$\frac{π}{6}$]（k∈Z）
18．设集合A={x|x＜0或x＞3}，B={x||x|＜2}，则A∩B=（　　）
A．（0，2）B．（-2，3）C．（-2，0）D．（2，3）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网