题目内容
.已知f(x)=x3+3ax2+bx+a2在x=-1时有极值0,求常数a,b的值.
.

 当a=1,b=3时,
当a=1,b=3时,
f′(x)=3x2+6x+3=3(x+1)2≥0,
∴f(x)在R上为增函数,无极值,故舍去.
当a=2,b=9时,
f′(x)=3x2+12x+9=3(x+1)(x+3),
当x∈(-∞,-3)时,f(x)为增函数;
当x∈(-3,-1)时,f(x)为减函数;
当x∈(-1,+∞)时,f(x)为增函数;
∴f(x)在x=-1时取得极小值.
∴a=2,b=9.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 ,
, 满足约束条件:
满足约束条件: 则
则 的最大值为( )
的最大值为( ) ,
, 且
且 ,
, ,则数列
,则数列 的前10项和为
的前10项和为 -
- <
< 成立,a,b应满足的条件是( )
成立,a,b应满足的条件是( )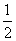 x2+bln (x+2)在(-1,+∞)上是减函数,则b的取值范围是 ( )
x2+bln (x+2)在(-1,+∞)上是减函数,则b的取值范围是 ( ) 的定义域为 .
的定义域为 . 在点(0,b)处的切线方程是
在点(0,b)处的切线方程是 ,则( )
,则( )