题目内容
在空间中,过点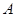 作平面
作平面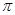 的垂线,垂足为
的垂线,垂足为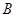 ,记
,记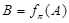 .设
.设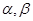 是两个不同的平面,对空间任意一点
是两个不同的平面,对空间任意一点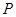 ,
,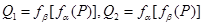 ,恒有
,恒有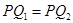 ,则( )
,则( )
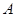 作平面
作平面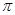 的垂线,垂足为
的垂线,垂足为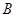 ,记
,记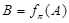 .设
.设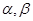 是两个不同的平面,对空间任意一点
是两个不同的平面,对空间任意一点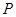 ,
,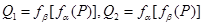 ,恒有
,恒有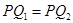 ,则( )
,则( )A.平面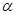 与平面 与平面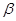 垂直 垂直 | B.平面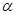 与平面 与平面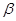 所成的(锐)二面角为 所成的(锐)二面角为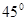 |
C.平面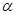 与平面 与平面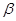 平行 平行 | D.平面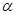 与平面 与平面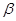 所成的(锐)二面角为 所成的(锐)二面角为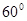 |
A
试题分析:令
 ,
, ,则
,则 ,即
,即 ,
, 。当平面
。当平面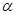 与平面
与平面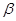 平行时,
平行时, 与
与 重合,
重合, 与
与 重合,因为
重合,因为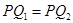 ,,所以P点到两个面的距离相等,与点P的任意性相矛盾,故C错。则
,,所以P点到两个面的距离相等,与点P的任意性相矛盾,故C错。则 ,由分析知
,由分析知 ,所以这五点共面设为
,所以这五点共面设为 ,设
,设 ,则
,则 三点共线,
三点共线, 三点共线,
三点共线, 即为
即为 所成二面角的平面角,由点P的任意性且恒有
所成二面角的平面角,由点P的任意性且恒有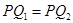 ,可知
,可知 三点重合,四边形
三点重合,四边形 为矩形,所以
为矩形,所以 ,即
,即 。故A正确。
。故A正确。
练习册系列答案
相关题目
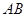 是圆的直径,
是圆的直径,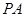 垂直圆所在的平面,
垂直圆所在的平面,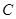 是圆上任一点,
是圆上任一点,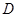 是线段
是线段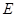 是线段
是线段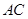 上的一点.
上的一点.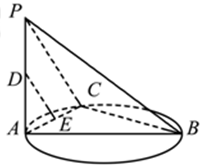
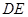 ∥平面
∥平面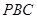 ;
;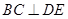 .
. ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE=x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE=x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .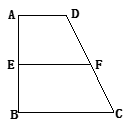
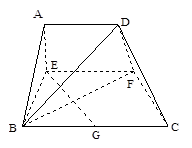
 中,
中,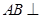 平面
平面 ,
,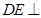 平面
平面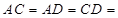
 ,
,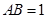 ,
,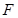 为
为 的中点.
的中点.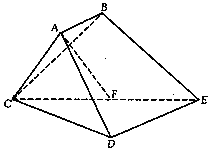
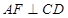 ;
;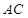 与平面
与平面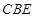 所成角的余弦值的大小.
所成角的余弦值的大小.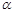 ,
,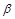 ,
,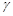 是三个不同的平面,给出下列命题:
是三个不同的平面,给出下列命题: 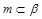 ,
, ,则
,则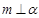 ;
;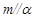 ,
,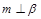 ,则
,则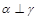 ,则
,则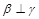 ;
;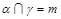 ,
,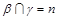 ,
,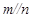 ,则
,则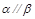 .
.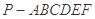 的底面是正六边形,
的底面是正六边形,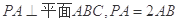 则下列结论正确的是( )
则下列结论正确的是( )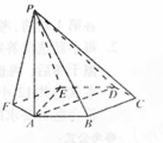
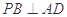


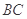 ∥
∥
 所成的角为45°
所成的角为45°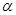 和
和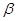 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: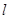 与
与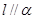 ;
;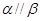 ;
;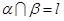 ,若
,若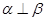 ;
;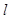 与平面
与平面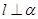 .
.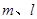 ,平面
,平面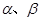 ,且
,且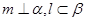 ,给出下列命题:
,给出下列命题: 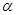 ∥
∥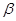 ,则m⊥
,则m⊥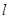 ; ②若
; ②若