题目内容
13．双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的左右焦点分别F1、F2，双曲线右支上一点P到F1的距离为11，则P到F2的距离为3．分析 根据双曲线方程求出a、b的值，再由双曲线的定义求出答案．
解答 解：由题意得，双曲线方程：$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1，
则a=4，b=3，
因为双曲线右支上一点P到F1的距离为11，
所以由双曲线的定义可得P到F2的距离为11-8=3，
故答案为：3．
点评 本题考查双曲线的标准方程以及定义的应用，属于基础题．
练习册系列答案
相关题目
3．对于下列表格所示的五个散点，若求得的线性回归直线方程为$\widehat{y}$=0.8x-155，
则实数m的值为8．
| x | 196 | 197 | 200 | 203 | 204 |
| y | 1 | 3 | 6 | 7 | m |
1．如图可能是下列哪个函数的图象（ ）
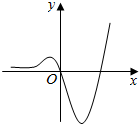
| A． | y=2x-x2-1 | B． | y=$\frac{x}{lnx}$ | C． | y=$\frac{{2}^{x}sinx}{{4}^{x}+1}$ | D． | y=（x2-2x）ex |
8．过抛物线y2=4x的焦点F的直线交抛物线于A，B两点，点O是原点，若|AF|=4，则△AOF的面积为（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{4\sqrt{3}}{3}$ | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |
18．M是椭圆$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1上一点，F1，F2是椭圆的左、右焦点，I是△MF1F2的内心，延长MI交F1F2于N，则$\frac{|MI|}{|IN|}$等于（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\sqrt{2}$ | C． | 2 | D． | 1 |
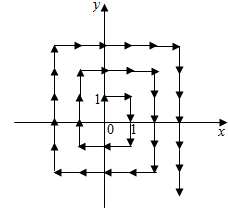如图，将自然数按如下规则“放置”在平面直角坐标系中，使其满足条件：①每个自然数“放置”在一个“整点”（横纵坐标均为整数的点）上；②0在原点，1在（0，1）点，2在（1，1）点，3在（1，0）点，4在（1，-1）点，5在（0，-1）点，…，即所有自然数按顺时针“缠绕”在以“0”为中心的“桩”上，则放置数字（2n+1）2，n∈N*的整点坐标是（-n，n+1）．