题目内容
9．若函数f（x）=a2-cosx（a∈R），则f'（x）等于（ ）| A． | sinx | B． | cosx | C． | 2a+sinx | D． | 2a-cosx |
分析 根据题意，由f（x）的解析式直接求导，即可得答案．
解答 解：根据题意，函数f（x）=a2-cosx，
则f'（x）=sinx；
故选：A．
点评 本题考查导数的计算，关键是掌握导数的计算公式．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
19．已知i为虚数单位，若复数z=$\frac{1-ai}{1+i}$（a∈R）的实部为-3，则|z|=（ ）
| A． | $\sqrt{10}$ | B． | 2$\sqrt{3}$ | C． | $\sqrt{13}$ | D． | 5 |
20．若集合A={x|x2≤4}，B={x|x≥0}．则A∩B=（ ）
| A． | {x|0≤x≤2} | B． | {x|x≥-2} | C． | {0，1，2} | D． | {1，2} |
17．在平面内的动点（x，y）满足不等式$\left\{\begin{array}{l}{x+y-3≤0}\\{x-y+1≥0}\end{array}\right.$，则z=2x+y的取值范围是（ ）
| A． | （-∞，+∞） | B． | （-∞，4] | C． | [4，+∞） | D． | [-2，2] |
4．设f（x）为可导函数，且f′（2）=$\frac{1}{2}$，求$\underset{lim}{h→0}$$\frac{f（2-h）-f（2+h）}{h}$的值（ ）
| A． | 1 | B． | -1 | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
14．已知函数f（x）=x2+ax+b（a，b∈R），记集合A={x∈R|f（x）≤0}，B={x∈R|f（f（x）+1）≤0}，若A=B≠∅，则实数a的取值范围为（ ）
| A． | [-4，4] | B． | [-2，2] | C． | [-2，0] | D． | [0，4] |
1．下列命题中正确的是（ ）
| A． | 终边在x轴负半轴上的角是零角 | |
| B． | 三角形的内角必是第一、二象限内的角 | |
| C． | 不相等的角的终边一定不相同 | |
| D． | 若β=α+k•360°（k∈Z），则α与β终边相同 |
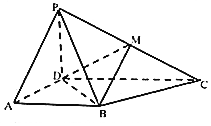如图，四棱锥P-ABCD中，平面PAD⊥平面ABCD，△PAD是正三角形，底面ABCD是直角梯形，AB∥CD，CD⊥AD，CD=2AB=2AD=2，M为PC的中点．