题目内容
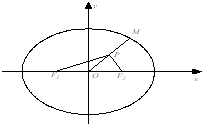 如图,M为椭圆
如图,M为椭圆| x2 |
| 3 |
| PF1 |
| PF2 |
-
| 7 |
| 4 |
-
.| 7 |
| 4 |
分析:由题意设出P的坐标,求出
,
,然后直接计算
•
,即可求出最小值.
| PF1 |
| PF2 |
| PF1 |
| PF2 |
解答:解:设M(
cosα ,sinα),所以P(
cosα ,
sinα),F1(-
,0),F2(
,0);
所以
=(-
-
cosα , -
sinα);
=(
-
cosα , -
sinα);
所以
•
=(-
-
cosα , -
sinα)• (
-
cosα , -
sinα)
=-2+
cos2α+
sin2α=
cos2 α-
≥-
.
•
的最小值-
.
故答案为:-
.
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
所以
| PF1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| PF2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
所以
| PF1 |
| PF2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=-2+
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 7 |
| 4 |
| 7 |
| 4 |
| PF1 |
| PF2 |
| 7 |
| 4 |
故答案为:-
| 7 |
| 4 |
点评:本题是中档题,考查椭圆的简单性质,椭圆的参数方程,向量的数量积等知识,考查计算能力.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 在平面直角坐标系xOy中,已知椭圆
在平面直角坐标系xOy中,已知椭圆 在矩形ABCD中,|AB|=2
在矩形ABCD中,|AB|=2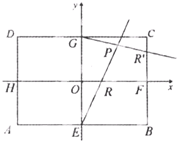 (2013•黄冈模拟)在矩形ABCD中,|AB|=2
(2013•黄冈模拟)在矩形ABCD中,|AB|=2 如图,已知A1,A2分别为椭圆
如图,已知A1,A2分别为椭圆