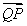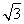题目内容
 +
+ =1上有两个动点P、Q,E(3,0),EP⊥EQ,则
=1上有两个动点P、Q,E(3,0),EP⊥EQ,则 •
• 的最小值为 .
的最小值为 .
【答案】分析:根据EP⊥EQ,和向量的数量积的几何意义,得∴ =
= =EP2,设出点P的坐标,利用两点间距离公式求出EP2,根据点P在椭圆上,代入消去y,转化为二次函数求最值问题,即可解得结果.
=EP2,设出点P的坐标,利用两点间距离公式求出EP2,根据点P在椭圆上,代入消去y,转化为二次函数求最值问题,即可解得结果.
解答:解:设P(x,y),则 ,即
,即 
∵EP⊥EQ,
∴ =
= =EP2,
=EP2,
而EP2=(x-3)2+y2= ,
,
∵-6≤x≤6
∴当x=4时,EP2=(x-3)2+y2= 有最小值6,
有最小值6,
故答案为:6.
点评:本题考查了向量在几何中的应用,以及向量数量积的几何意义,和椭圆的有界性,二次函数求最值等基础知识,注意椭圆的有界性,考查学生灵活应用知识分析解决问题的能力.
 =
= =EP2,设出点P的坐标,利用两点间距离公式求出EP2,根据点P在椭圆上,代入消去y,转化为二次函数求最值问题,即可解得结果.
=EP2,设出点P的坐标,利用两点间距离公式求出EP2,根据点P在椭圆上,代入消去y,转化为二次函数求最值问题,即可解得结果.解答:解:设P(x,y),则
 ,即
,即 
∵EP⊥EQ,
∴
 =
= =EP2,
=EP2,而EP2=(x-3)2+y2=
 ,
,∵-6≤x≤6
∴当x=4时,EP2=(x-3)2+y2=
 有最小值6,
有最小值6,故答案为:6.
点评:本题考查了向量在几何中的应用,以及向量数量积的几何意义,和椭圆的有界性,二次函数求最值等基础知识,注意椭圆的有界性,考查学生灵活应用知识分析解决问题的能力.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目