Question

【题目】【2016高考北京文数】已知椭圆C：过点A（2,0），B（0,1）两点.

（I）求椭圆C的方程及离心率；

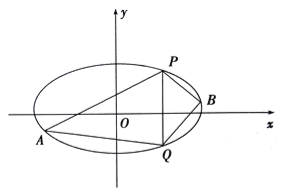
（Ⅱ）设P为第三象限内一点且在椭圆C上，直线PA与y轴交于点M，直线PB与x轴交于点N，求证：四边形ABNM的面积为定值.

Answer 1

【答案】（Ⅰ）；（Ⅱ）见解析.

【解析】

试题分析：（Ⅰ）根据两顶点坐标可知a,b的值，则亦知椭圆方程，根据椭圆性质及离心率公式求解；（Ⅱ）四边形的面积等于对角线乘积的一半，分别求出对角线的值求乘积为定值即可.

试题解析：（I）由题意得，，．

所以椭圆的方程为．

又，

所以离心率．

（II）设（，），则．

又，，所以，

直线的方程为．

令，得，从而．

直线的方程为．

令，得，从而．

所以四边形的面积

．

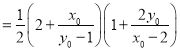
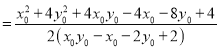
从而四边形的面积为定值．