题目内容
(本小题满分16分)在平面直角坐标系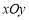 中,已知椭圆
中,已知椭圆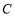 :
: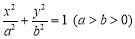 的离心率
的离心率 ,直线
,直线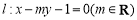 过椭圆
过椭圆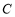 的右焦点
的右焦点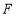 ,且交椭圆
,且交椭圆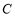 于
于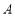 ,
,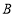 两点.
两点.
(1)求椭圆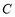 的标准方程;
的标准方程;
(2)已知点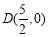 ,连结
,连结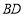 ,过点
,过点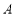 作垂直于
作垂直于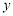 轴的直线
轴的直线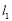 ,设直线
,设直线 与直线
与直线 交于点
交于点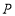 ,试探索当
,试探索当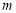 变化时,是否存在一条定直线
变化时,是否存在一条定直线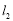 ,使得点
,使得点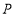 恒在直线
恒在直线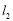 上?若存在,请求出直线
上?若存在,请求出直线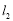 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(1)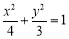 (2)点
(2)点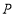 恒在直线
恒在直线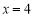 上
上
【解析】
试题分析:(1)直线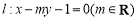 与x轴的交点为椭圆
与x轴的交点为椭圆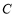 的右焦点
的右焦点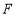 ,所以
,所以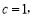 由
由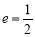 得
得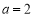 从而
从而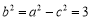 ,所以椭圆
,所以椭圆 的标准方程为
的标准方程为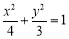 .(2)探索性问题,先通过特殊情形探索目标:令
.(2)探索性问题,先通过特殊情形探索目标:令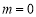 ,则根据对称性知满足题意的定直线
,则根据对称性知满足题意的定直线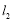 只能是
只能是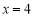 .问题转化为证明P,B,D三点共线,可利用斜率相等进行证明:设
.问题转化为证明P,B,D三点共线,可利用斜率相等进行证明:设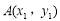 ,
, ,则
,则 ,从而
,从而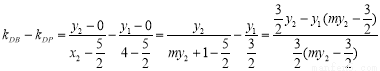
 ,再利用直线与椭圆方程联立方程组得关于y的一元二次方程,由韦达定理得
,再利用直线与椭圆方程联立方程组得关于y的一元二次方程,由韦达定理得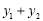 与
与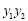 关系,进而得
关系,进而得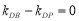
试题解析:(1)由题设,得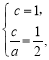 解得
解得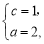 从而
从而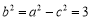 ,
,
所以椭圆 的标准方程为
的标准方程为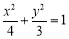 . 4分
. 4分
(2)令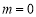 ,则
,则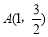 ,
,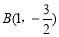 或者
或者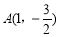 ,
,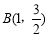 .
.
当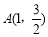 ,
,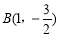 时,
时,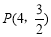 ;当
;当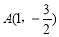 ,
,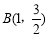 时,
时,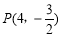 ,
,
所以,满足题意的定直线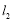 只能是
只能是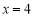 . 6分
. 6分
下面证明点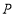 恒在直线
恒在直线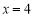 上.
上.
设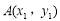 ,
, ,由于
,由于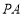 垂直于
垂直于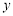 轴,所以点
轴,所以点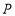 的纵坐标为
的纵坐标为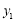 ,从而只要证明
,从而只要证明 在直线
在直线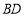 上. 8分
上. 8分
由 得
得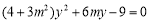 ,
,
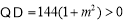 ,
,
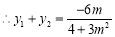 ,
,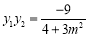 .① 10分
.① 10分
∵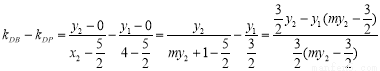
 , 13分
, 13分
①式代入上式,得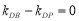 , 所以
, 所以 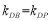 . 15分
. 15分
∴点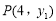 恒在直线
恒在直线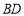 上,从而直线
上,从而直线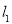 、直线
、直线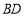 与直线
与直线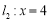 三线恒过同一点
三线恒过同一点
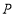 , 所以存在一条定直线
, 所以存在一条定直线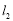 :
: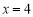 使得点
使得点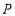 恒在直线
恒在直线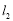 上. 16分
上. 16分
考点:直线与椭圆位置关系
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
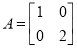 ,
,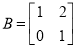 ,若矩阵
,若矩阵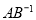 对应的变换把直线
对应的变换把直线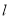 变为直线
变为直线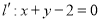 ,求直线
,求直线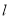 的方程.
的方程. ,则
,则 .
. 的定义域为 .
的定义域为 .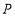 ,
,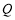 分别在两条直线
分别在两条直线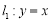 和
和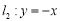 上运动,且它们的横坐标分别为角
上运动,且它们的横坐标分别为角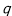 的正弦,余弦,
的正弦,余弦,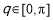 .记
.记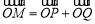 ,求动点
,求动点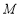 的轨迹的普通方程.
的轨迹的普通方程. 对任意满足
对任意满足 的实数
的实数 恒成立,则实数
恒成立,则实数 的最大值为 .
的最大值为 . 的值是 .
的值是 .
 中,
中, ,
, ,
, ,则
,则 _______.
_______. 中,角
中,角 ,
,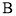 ,
, 所对的边分别为
所对的边分别为 ,
,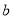 ,
, ,且满足
,且满足 .
.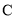 的大小;
的大小;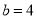 ,
, ,求边长
,求边长 的值.
的值.