题目内容
各项均为正数的数列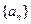 ,
,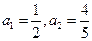 ,且对满足
,且对满足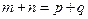 的任意正整
的任意正整
数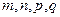 都有
都有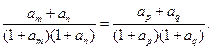
(I)求通项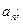
(II)记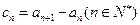 ,设数列
,设数列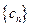 的前
的前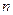 项和为
项和为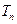 ,求证:对任意正整数
,求证:对任意正整数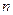 都有
都有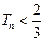 。
。
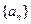 ,
,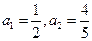 ,且对满足
,且对满足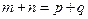 的任意正整
的任意正整数
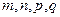 都有
都有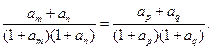
(I)求通项
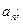
(II)记
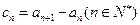 ,设数列
,设数列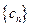 的前
的前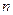 项和为
项和为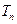 ,求证:对任意正整数
,求证:对任意正整数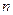 都有
都有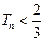 。
。(I)解法一:特征根法,令 得
得

 再利用构造新数列求通项公式
再利用构造新数列求通项公式
设


 又
又 



解法二:由 得
得
 将
将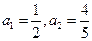 代入化简得
代入化简得

所以
故数列 为等比数列,从而
为等比数列,从而
 即
即
可验证, 满足题设条件.
满足题设条件.
(II)



 得
得

 再利用构造新数列求通项公式
再利用构造新数列求通项公式设



 又
又 



解法二:由
 得
得  将
将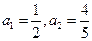 代入化简得
代入化简得 
所以

故数列
 为等比数列,从而
为等比数列,从而 即
即
可验证,
 满足题设条件.
满足题设条件.(II)




略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
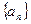 中,
中,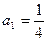 ;
;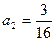 ,对任意的
,对任意的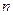 为正整数都有
为正整数都有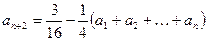 。
。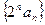 是等差数列;
是等差数列;
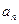 ;
;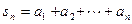 (
(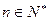 ),是否存在实数
),是否存在实数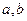 使得
使得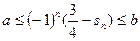 对任意的
对任意的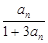 ,a1=2,则a4为 ( )
,a1=2,则a4为 ( )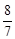
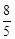
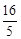
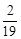
 }中,已知
}中,已知
 ,
, ,
, ,则
,则 是( )
是( )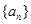 为等差数列,
为等差数列,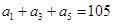 ,
,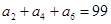 ,则
,则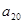 等于( )
等于( )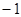
 的前
的前 项和
项和 ,则
,则 =
=  ,圆
,圆 和圆
和圆 若
若 平分
平分 的周长,则
的周长,则 的所有项和为
的所有项和为 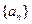 中,
中, 首项
首项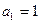 ,数列
,数列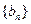 满足
满足 则数列
则数列 (
( ),①如果
),①如果 ,那么
,那么 =
=

 4;
4; ,那么
,那么 =
=

 ,那么
,那么